A definição científica do trabalho difere em alguns aspectos de seu significado cotidiano. Certas coisas que consideramos trabalhosas, como fazer uma prova ou carregar uma carga pesada no nível do chão, não funcionam como definido por um cientista. A definição científica do trabalho revela sua relação com a energia – sempre que o trabalho é feito, a energia é transferida.

Para o trabalho, no sentido científico, a ser feito, uma força deve ser exercida e deve haver deslocamento na direção da força.

Formalmente, o trabalho feito em um sistema por uma força constante é definido como sendo o produto do componente da força na direção do movimento vezes a distância pela qual a força atua. Para o movimento unidirecional em uma dimensão, isso é expresso na forma de equação:

onde está o trabalho, é o deslocamento do sistema, e é o ângulo entre o vetor de força e o vetor de deslocamento. Nós também podemos escrever isso como:

Para encontrar o trabalho realizado em um sistema que passa por um movimento que não é unidirecional ou que está em duas ou três dimensões, dividimos o movimento em segmentos unidimensionais unidirecionais e somamos o trabalho realizado em cada segmento.

O Que é Trabalho?

O trabalho realizado em um sistema por uma força constante é o produto do componente da força na direção do movimento vezes a distância através da qual a força atua. Para o movimento unidirecional em uma dimensão, isso é expresso na forma da equação:

onde W é o trabalho, F é a magnitude da força no sistema, d é a magnitude do deslocamento do sistema e 0 é o ângulo entre o vetor de força, F é o vetor de deslocamento d.

Cálculo do Trabalho

Trabalho e energia têm as mesmas unidades. A partir da definição do trabalho, vemos que essas unidades são distâncias forçadas. Assim, nas unidades do SI, o trabalho e a energia são medidos em newton-metros. Um medidor de newton recebe o nome especial joule (J) e 1 J = 1 N . m = 1 kg . m² / s². Um joule não é uma grande quantidade de energia; levantaria uma pequena maçã de 100 gramas a uma distância de cerca de 1 metro.

Matematicamente, o trabalho pode ser expresso pela seguinte equação:

W = F • d • cos Θ

onde F é a força, d é o deslocamento e o ângulo ( teta ) é definido como o ângulo entre a força e o vetor de deslocamento. Talvez o aspecto mais difícil da equação acima seja o ângulo “teta”. O ângulo não é apenas um ângulo ole , mas sim um ângulo muito específico. A medida do ângulo é definida como o ângulo entre a força e o deslocamento. Para obter uma ideia do seu significado, considere os três cenários a seguir.

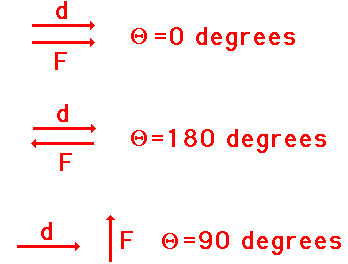
Cenário A: Uma força age diretamente sobre um objeto quando é deslocada para a direita. Nesse caso, o vetor de força e o vetor de deslocamento estão na mesma direção. Assim, o ângulo entre F e d é 0 graus.

Cenário B: Uma força age à esquerda sobre um objeto que é deslocado para a direita. Nesse caso, o vetor de força e o vetor de deslocamento estão na direção oposta. Assim, o ângulo entre F e d é de 180 graus.

Cenário C: Uma força age para cima em um objeto quando é deslocado para a direita. Nesse caso, o vetor de força e o vetor de deslocamento são perpendiculares entre si. Assim, o ângulo entre F e d é de 90 graus.

Vamos considerar o Cenário C acima com mais detalhes. Cenário C envolve uma situação semelhante ao garçom que carregou uma bandeja cheia de refeições acima da cabeça por um braço em linha reta através da sala a uma velocidade constante. Foi mencionado anteriormente que o garçom não trabalha na bandeja enquanto ele a carrega pela sala. A força fornecida pelo garçom na bandeja é uma força para cima e o deslocamento da bandeja é um deslocamento horizontal. Como tal, o ângulo entre a força e o deslocamento é de 90 graus. Se o trabalho feito pelo garçom na bandeja fosse calculado, então os resultados seriam 0. Independentemente da magnitude da força e do deslocamento, F * d * cosseno 90 graus é 0 (já que o cosseno de 90 graus é 0 ). Uma força vertical nunca pode causar um deslocamento horizontal; assim, uma força vertical não funciona em um objeto deslocado horizontalmente.

Pode-se notar com precisão que a mão do garçom empurrou a bandeja para frente por um breve período de tempo para acelerá-la do repouso para uma velocidade final de caminhada. Mas uma vez até a velocidade, a bandeja permanecerá em seu movimento em linha reta a uma velocidade constante sem uma força para a frente. E se a única força exercida sobre a bandeja durante o estágio de velocidade constante de seu movimento é para cima, então nenhum trabalho é feito na bandeja. Novamente, uma força vertical não funciona em um objeto deslocado horizontalmente.

A equação para o trabalho lista três variáveis ​​- cada variável está associada a uma das três palavras-chave mencionadas na definição de trabalho (força, deslocamento e causa). O ângulo teta na equação está associado à quantidade de força que causa um deslocamento. Como mencionado em uma unidade anterior. Quando uma força é exercida sobre um objeto em um ângulo em relação à horizontal, apenas uma parte da força contribui para (ou causa) um deslocamento horizontal. Vamos considerar a força de uma corrente puxando para cima e para a direita sobre Fido, a fim de arrastar Fido para a direita. É apenas o componente horizontal da força de tensão na corrente que faz com que o Fido seja deslocado para a direita. O componente horizontal é encontrado multiplicando a força F pelo cosseno do ângulo entre F e d. Nesse sentido, o cosseno teta na equação do trabalho relaciona-se ao fator causa – seleciona a porção da força que realmente causa um deslocamento.

O Significado do Trabalho Negativo

Ocasionalmente, uma força atua sobre um objeto em movimento para impedir um deslocamento. Os exemplos podem incluir um carro derrapando até parar em uma superfície da estrada ou um corredor de beisebol deslizando até parar na terra do campo. Em tais casos, a força atua na direção oposta ao movimento dos objetos, a fim de retardá-lo. A força não causa o deslocamento, mas o impede. Essas situações envolvem o que é comumente chamado de trabalho negativo. O negativo de trabalho negativo refere-se ao valor numérico que resulta quando os valores de F, d e teta são substituídos na equação de trabalho. Como o vetor de força é diretamente oposto ao vetor de deslocamento, theta é de 180 graus. O cosseno (180 graus) é -1 e, portanto, um valor negativo resulta da quantidade de trabalho realizado no objeto. 

Unidades de Trabalho

Sempre que uma nova quantidade é introduzida na física, as unidades métricas padrão associadas a essa quantidade são discutidas. No caso do trabalho (e também energia), a unidade métrica padrão é o Joule (abreviado como J ). Um Joule é equivalente a um Newton de força causando um deslocamento de um metro. Em outras palavras:

O Joule é a unidade de trabalho.

1 Joule = 1 Newton * 1 metro

1 J = 1 N * m

De fato, qualquer unidade de força multiplicada por qualquer unidade de deslocamento é equivalente a uma unidade de trabalho. Algumas unidades não padrão para o trabalho são mostradas abaixo. Observe que, quando analisado, cada conjunto de unidades é equivalente a uma unidade de força vezes uma unidade de deslocamento.

Unidades de trabalho não padronizadas:

pé • libra

kg • (m / s 2 ) • m

kg • (m 2 / s 2 )

Em resumo, o trabalho é feito quando uma força atua sobre um objeto para causar um deslocamento. Três quantidades devem ser conhecidas para calcular a quantidade de trabalho. Essas três grandezas são força, deslocamento e o ângulo entre a força e o deslocamento.