A regra de três simples é uma maneira de descobrir um valor a partir de outros três conhecidos, divididos em pares relacionados cujos valores têm mesma grandeza e unidade. Além da regra de três simples existe também a regra de três composta.
Alguns dos passos utilizados numa regra de três simples:
1º) Construir uma tabela, agrupando as grandezas da mesma espécie em colunas e mantendo na mesma linha as grandezas de espécies diferentes em correspondência.
2º) Identificar se as grandezas são diretamente ou inversamente proporcionais.
3º) Montar a proporção e resolver a equação.
Regra de três simples direta:
Quando temos duas grandezas diretamente proporcionais, ou seja, quando a variação de um deles é semelhante a variação no outro, aumentando ou diminuindo.
Exemplos
Exemplo 1
Em dois litros de água foram misturados 150 gramas de certa substância para se obter uma mistura homogênea. Calcule quantos gramas deverão ser adicionadas em 1,2 litros de água para que a mistura continue no padrão homogênea.
| Litros de Água | Substância (g) |
| 2 | 150 |
| 1,2 | x |
Grandezas diretamente proporcionais:
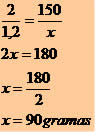
Exemplo 2
Em um evento houve, em média, 1111 pessoas para cada 2m² de área. Se sabemos que o show ocorreu em um local com 2700m², é possível calcular quantas pessoas assistiram ao show com a regra de três.
| Pessoas | Área (m2)(m2) |
|---|---|
| 11 | 2 |
| x | 2700 |
Quanto mais área, mais pessoas, portanto são diretamente proporcionais; podemos multiplicar em cruz os valores da tabela:
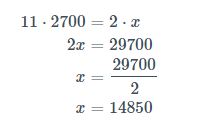
Portanto 1485014850 pessoas assistiram ao show.
Exemplo 3: conversão de unidades
Uma das utilidades da regra de três é a de converter unidades. Se o comprimento de 1 polegada é aproximadamente 2,5cm, qual é a medida de 15,5cm em polegadas?
Uma das utilidades da regra de três é a de converter unidades. Se o comprimento de 11 polegada é aproximadamente 2,5cm qual é a medida de 15,5cm em polegadas?
| Polegadas | Centímetros |
|---|---|
| 1 | 2,5 |
| x | 15,5 |
Quanto mais polegadas, mais centímetros, portanto as medidas são diretamente proporcionais e devemos multiplicar em cruz.
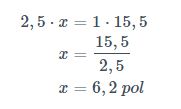
Portanto, 15,5cm correspondem a aproximadamente 6,2 pol.
Exemplo 4: unidades diferentes
A cada 15min passam 2 ônibus em certo ponto da cidade. Como exemplo, iremos aplicar a regra de três para calcular quantos ônibus passam neste ponto em um período de 2 horas e meia.
Primeiro, colocamos os valores na tabela:
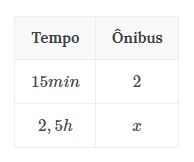
O problema é que os valores de tempo não estão na mesma unidade, o que significa que a proporção ficará incorreta. O caminho mais fácil é transformar 2,5h em minutos. Como cada hora possui 60 minutos, basta multiplicar por 60:
2,5h⋅60=150min
Agora alteramos o valor na tabela e continuamos a resolução:
| Tempo | Ônibus |
|---|---|
| 15min | 2 |
| 150min | x |
Quanto mais tempo, mais ônibus passam pelo ponto, portanto é um caso de proporção direta; multiplicamos os valores em cruz e resolvemos a equação:
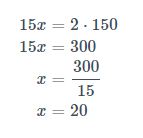
Portanto, em 2 horas e meia, passam 20 ônibus pelo ponto.
Exemplo 5: proporção inversa
Marcela irá gastar 4 horas para fazer uma viagem se mantiver uma velocidade de 90km/h. Se ela desejar fazer a viagem em 1 hora a menos, que velocidade deverá manter?
Este é um problema de proporção inversa, pois quanto mais velocidade, menor é o tempo da viagem. Portanto, ao fazer a tabela, iremos multiplicar os valores em linha.
| Tempo | Velocidade |
|---|---|
| 44 | 9090 |
| 33 | x |
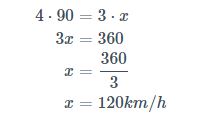
Portanto ela deverá manter uma velocidade de 120km/h se quiser fazer a viagem em 3 horas.
Exemplo 6: divisão de gastos
9 amigos pediram pizza e cada um deveria pagar R$11,20, mas 2 deles precisaram levar a avó no jiu-jitsu e não vão dividir a conta. Podemos calcular quanto cada um do restantes deve pagar através de uma regra de três.
A proporção é inversa, primeiro porque o que os 9 iriam pagar é o mesmo que os 7 restantes deverão pagar (valor constante) e porque com menos gente, cada um deve pagar mais.
Note que não colocaremos o número 2 na tabela, quem entra são os 7 restantes.
| Pessoas | Valor |
|---|---|
| 9 | 11,20 |
| 7 | x |
Como a proporção é inversa, multiplicamos em linha.
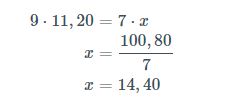
Cada um deverá pagar R$14,40 agora.
Exemplo 7: regra de “dois”
Podemos resolver um problema de proporção conhecendo apenas 2 valores se os outros 2 possuírem uma relação entre si. Um exemplo disso é o seguinte problema:
“Uma Gráfica possui certo número de impressoras e conseguia imprimir 1500 livros por dia. Agora, com 2 impressoras a mais, consegue imprimir 1800 livros por dia. Quantas máquinas esta editora possui agora?”
Para resolvê-lo, iremos chamar de x quantas impressoras ela possuía:
x: quantas impressoras a editora tinha
Então, significa que:
(x+2): quantas impressoras a editora tem
Colocando as informações na tabela:
| Impressoras | Livros |
|---|---|
| x | 1500 |
| (x+2) | 1800 |
A proporção é direta, portanto multiplicamos os valores em cruz; preste atenção nos parênteses
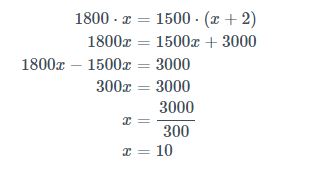
Portanto a gráfica possuía 10 impressoras e agora possui 12.
A História da Regra de 3
Gregos e romanos já estudavam as relações entre proporções, porém não chegaram a aplicá-las na resolução de problemas. Foram os árabes na idade média que trouxeram a regra de três. Leonardo de Pisa no século XIII em seu livro Liber Abaci, difundiu os princípios desse método, dando-o o nome que conhecemos hoje como “Regra de Três Números Conhecidos”.