A matemática é a ciência que lida com a lógica da forma, quantidade e arranjo. A matemática está ao nosso redor, em tudo que fazemos. É o alicerce de tudo em nossas vidas diárias, incluindo dispositivos móveis, arquitetura (antiga e moderna), arte, dinheiro, engenharia e até mesmo esportes.
Desde o início da história registrada, a descoberta da matemática tem estado à frente de toda sociedade civilizada e em uso até nas culturas mais primitivas. As necessidades da matemática surgiram com base nas necessidades da sociedade. Quanto mais complexa é uma sociedade, mais complexas são as necessidades matemáticas. As tribos primitivas precisavam de pouco mais que a capacidade de contar, mas também se baseavam na matemática para calcular a posição do sol e a física da caça.

História da Matemática
Várias civilizações – na China, Índia, Egito, América Central e Mesopotâmia – contribuíram para a matemática como a conhecemos hoje. Os sumérios foram os primeiros a desenvolver um sistema de contagem. Os matemáticos desenvolveram aritmética, que inclui operações básicas, multiplicação, frações e raízes quadradas. O sistema dos sumérios passou pelo Império acadiano para os babilônios por volta de 300 aC Seiscentos anos depois, na América, os maias desenvolveram elaborados sistemas de calendário e eram astrônomos habilidosos. Nessa época, o conceito de zero foi desenvolvido.
Com o desenvolvimento das civilizações, os matemáticos começaram a trabalhar com a geometria, que calcula áreas e volumes para fazer medições angulares e tem muitas aplicações práticas. A geometria é usada em tudo, desde construção de casas até moda e design de interiores.

A geometria andava de mãos dadas com a álgebra, inventada no século IX por um matemático persa, Mohammed ibn-Musa al-Khowarizmi. Ele também desenvolveu métodos rápidos para multiplicar e mergulhar números, que são conhecidos como algoritmos – uma corrupção de seu nome.
A álgebra oferecia às civilizações uma maneira de dividir heranças e alocar recursos. O estudo da álgebra significava que os matemáticos estavam resolvendo equações lineares e sistemas, bem como quadráticas, e se aprofundando em soluções positivas e negativas. Os matemáticos da antiguidade também começaram a olhar para a teoria dos números. Com origens na construção da forma, a teoria dos números analisa números figurados, a caracterização de números e teoremas.
Os Gregos e a Matemática
O estudo da matemática nas primeiras civilizações foi o alicerce para a matemática dos gregos, que desenvolveram o modelo da matemática abstrata através da geometria. A Grécia, com sua incrível arquitetura e complexo sistema de governo, foi o modelo de realização matemática até os tempos modernos.

Matemáticos gregos foram divididos em várias escolas:
- A Escola Jônica, fundada por Thales, que é frequentemente creditada por ter dado as primeiras provas dedutivas e desenvolver cinco teoremas básicos em geometria plana.
- A Escola Pitagórica, fundada por Pitágoras, que estudou a proporção, a geometria sólida e plana e a teoria dos números.
- A Escola Eleática, que incluía Zeno de Elea, famosa por seus quatro paradoxos.
- A Escola Sofista, que é creditada por oferecer ensino superior nas cidades gregas avançadas. Os sofistas deram instruções sobre o debate público usando o raciocínio abstrato.
- A Escola Platônica, fundada por Platão, encorajou a pesquisa em matemática em um ambiente muito parecido com uma universidade moderna.
- A Escola de Eudoxo, fundada por Eudoxo, que desenvolveu a teoria da proporção e magnitude e produziu muitos teoremas na geometria plana
- A Escola de Aristóteles, também conhecida como Liceu, foi fundada por Aristóteles e seguiu a escola platônica.
Além dos matemáticos gregos listados acima, vários gregos fizeram uma marca indelével na história da matemática. Arquimedes, Apolônio, Diofante, Pappus e Euclides vieram da época. Para entender melhor a sequência e como esses matemáticos influenciaram uns aos outros, visite esta linha do tempo.

Durante esse tempo, os matemáticos começaram a trabalhar com trigonometria. De natureza computacional, a trigonometria requer a medição de ângulos e o cálculo de funções trigonométricas, que incluem seno, cosseno, tangente e seus recíprocos. Trigonometria baseia-se na geometria sintética desenvolvida por matemáticos gregos como Euclides. Por exemplo, o teorema de Ptolomeu fornece regras para os acordes da soma e da diferença de ângulos, que correspondem às fórmulas de soma e diferença para senos e cossenos. Nas culturas passadas, a trigonometria foi aplicada à astronomia e ao cálculo de ângulos na esfera celeste.
Após a queda de Roma, o desenvolvimento da matemática foi assumido pelos árabes, depois pelos europeus. Fibonacci foi um dos primeiros matemáticos europeus e famoso por suas teorias sobre aritmética, álgebra e geometria. O Renascimento levou a avanços que incluíam frações decimais, logaritmos e geometria projetiva. A teoria dos números foi grandemente expandida, e teorias como probabilidade e geometria analítica inauguraram uma nova era da matemática, com o cálculo na vanguarda.
Desenvolvimento de Cálculo
No século XVII, Isaac Newton e Gottfried Leibniz desenvolveram independentemente as bases para o cálculo. O desenvolvimento do cálculo passou por três períodos: antecipação, desenvolvimento e rigorização. No estágio de antecipação, os matemáticos tentavam usar técnicas que envolviam processos infinitos para encontrar áreas sob curvas ou maximizar certas qualidades. No estágio de desenvolvimento, Newton e Leibniz reuniram essas técnicas através da derivada e integral. Embora seus métodos nem sempre fossem logicamente corretos, os matemáticos do século XVIII assumiram o estágio de rigor e conseguiram justificá-los e criar o estágio final do cálculo. Hoje, definimos a derivada e integral em termos de limites.

Em contraste com o cálculo, que é um tipo de matemática contínua, outros matemáticos adotaram uma abordagem mais teórica. A matemática discreta é o ramo da matemática que lida com objetos que podem assumir apenas um valor distinto e separado. Objetos discretos podem ser caracterizados por inteiros, enquanto objetos contínuos requerem números reais. A matemática discreta é a linguagem matemática da ciência da computação, pois inclui o estudo de algoritmos. Os campos da matemática discreta incluem a combinatória, a teoria dos grafos e a teoria da computação.
As pessoas frequentemente se perguntam o que os matemáticos de relevância servem hoje. Em um mundo moderno, a matemática aplicada, como a matemática, não é apenas relevante, é crucial. A matemática aplicada é o ramo da matemática que está envolvido no estudo do mundo físico, biológico ou sociológico. A ideia da matemática aplicada é criar um grupo de métodos que resolvam problemas na ciência. Áreas modernas de matemática aplicada incluem física matemática, biologia matemática, teoria de controle, engenharia aeroespacial e finanças de matemática. Não só a matemática aplicada resolve problemas, mas também descobre novos problemas ou desenvolve novas disciplinas de engenharia. Matemáticos aplicados exigem experiência em muitas áreas de matemática e ciências, intuição física, bom senso e colaboração. A abordagem comum na matemática aplicada é construir um modelo matemático de um fenômeno,

Embora não seja necessariamente um oposto à matemática aplicada, a matemática pura é impulsionada por problemas abstratos, e não por problemas do mundo real. Muito do que é perseguido pelos matemáticos puros pode ter suas raízes em problemas físicos concretos, mas uma compreensão mais profunda desses fenômenos traz problemas e tecnicismos. Esses problemas abstratos e técnicos são o que a matemática pura tenta resolver, e essas tentativas levaram a grandes descobertas para a humanidade, incluindo a Universal Turing Machine, teorizada por Alan Turing em 1937. A Máquina Universal de Turing, que começou como uma idéia abstrata, mais tarde lançou as bases para o desenvolvimento do computador moderno. A matemática pura é abstrata e baseada na teoria e, portanto, não é restringida pelas limitações do mundo físico.
De acordo com um matemático puro, matemáticos puros provam teoremas e matemáticos aplicados constroem teorias. Puro e aplicado não são mutuamente exclusivos, mas estão enraizados em diferentes áreas de matemática e resolução de problemas. Embora a matemática complexa envolvida na matemática pura e aplicada esteja além do entendimento da maioria dos americanos comuns, as soluções desenvolvidas a partir dos processos afetaram e melhoraram a vida de todos.

Jogos Matemáticos
Os jogos de matemática, ou jogos matemáticos, incluem muitos temas que fazem parte da matemática recreativa. O que distingue um jogo matemático de outro jogo comum é a ênfase na análise matemática do jogo, a lógica necessária para a sua realização, e não a maneira de jogar.
Sudoku
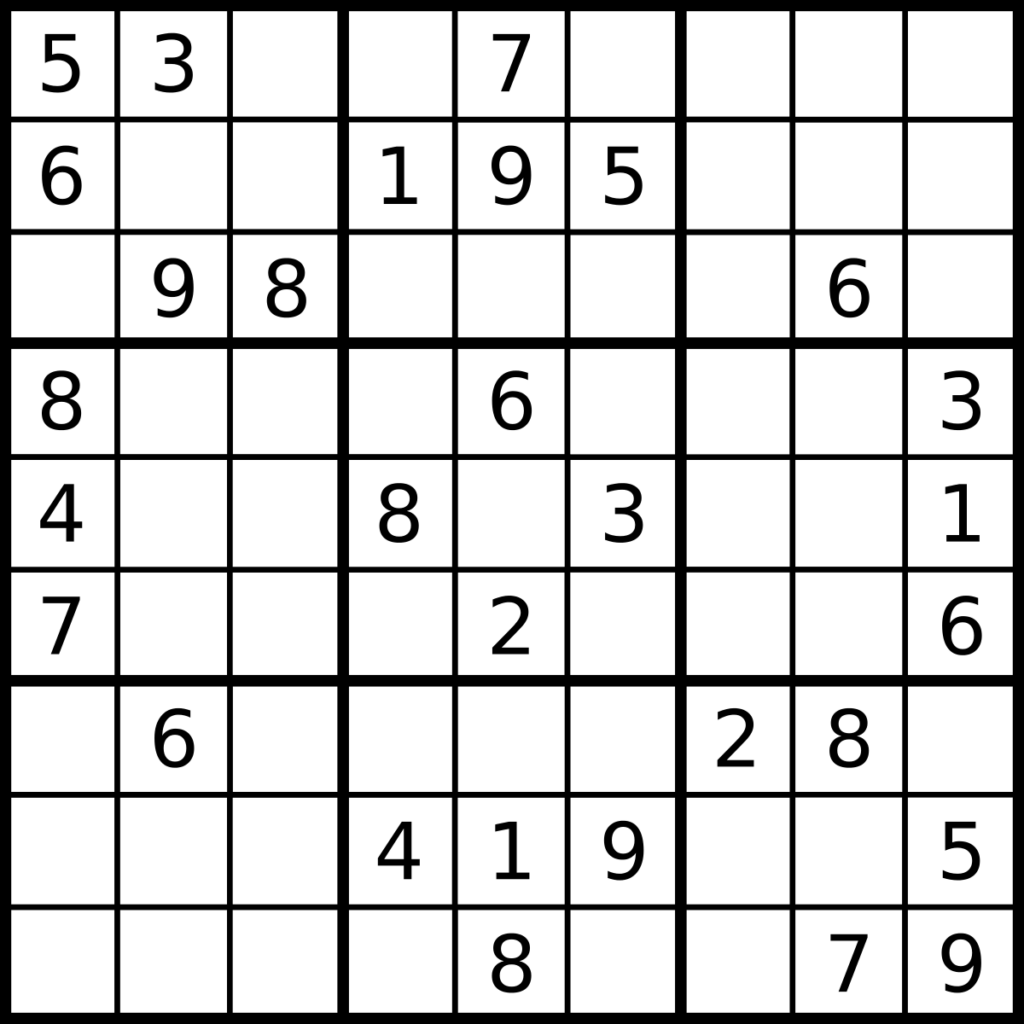
Sudoku é um gênero de quebra-cabeças lógicos que utiliza quadrados numerados. Na versão convencional, o objetivo consiste em preencher uma grade de 9 x 9 com os pontos de 1 a 9, de modo que cada dígito em cada unidade (coluna, linha bloco = 3 × 3 sub-quadrado) aparece apenas uma vez – e em cada um dos 81 campos ocorre exatamente um dígito. O ponto de partida é uma grade na qual vários dígitos já foram especificados. Enigmas de Sudoku são publicados regularmente em jornais e revistas até os dias de hoje.
Os numerais no jogo sudoku são usados por comodidade; as relações aritméticas entre numerais são absolutamente irrelevantes (não requer lógica para cálculos matemáticos). Qualquer combinação de símbolos distintos como letras, formas, ou cores podem ser usadas no jogo sem alterar as regras.
A atração do jogo é que as regras são simples, contudo, a linha de raciocínio requerida para alcançar a solução pode ser complexa. O sudoku é recomendado por alguns educadores como um exercício para o pensamento lógico. O nível de dificuldade pode ser selecionado para combinar com o público. Existem diversas fontes na internet não ligadas a editoras que disponibilizam os jogos gratuitamente.
Seu formato é mais frequentemente uma grade de 9×9 constituída de sub-grades de 3×3 chamadas de “regiões” (outros termos incluem “caixas” e “blocos”; algumas vezes, o termo “quadrante” é utilizado, apesar de ser um termo impreciso para uma grade de 3×3). Algumas células já contém números, chamadas “números dados” (ou, algumas vezes, “pistas”). O objetivo é preencher as células vazias com um número em cada célula, de maneira que cada coluna, linha e região contenha os números de 1 a 9 apenas uma vez. Na solução do jogo, cada número aparece apenas uma vez em qualquer um dos sentidos ou regiões; daí, o termo sudoku, que significa “únicos números”.
Torre de Hanói
A torres de Hanói é um jogo de paciência e quebra-cabeças matemáticos. O jogo consiste em três barras iguais A , B e C , nas quais são colocados vários discos perfurados, todos de tamanhos diferentes. No início, todas as fatias são colocadas no palito A, ordenadas por tamanho, com a fatia maior na parte inferior e a menor na parte superior. O objetivo do jogo é mover toda a pilha de discos de A para C.

Para cada volta, o disco mais alto de qualquer barra pode ser colocado em cima de uma das outras duas barras, desde que não exista um disco menor ali. Consequentemente, em cada ponto do jogo, as fatias de cada peça são ordenadas por tamanho.
Provavelmente o jogo foi inventado em 1883 pelo matemático francês Édouard Lucas – às vezes chamado de Torres Lucas (Inglês Lucas Tower ). Pensou na história de que os monges indianos no grande templo de Benares, no centro do mundo, teriam de mover uma torre de 64 discos de ouro e, se tivessem conseguido, o fim do mundo teria chegado.
Ouri
Ouri é um jogo destinado a duas pessoas e é jogado em um tabuleiro de 12 casas com 48 pedras. A maior diferença da mancala tradicional é que neste jogo nenhuma pedra é colocada no Mancalas (“comida de pedra”) dos jogadores. Somente quando a última pedra é lançada ao lado do inimigo e nesta casa podem ser coletadas 2 ou 3 pedras. Neste caso, todas as pedras das casas anteriores são coletadas desde que sejam 2 ou 3. O objetivo do jogo é coletar mais sementes do que seu oponente. Todas as sementes têm o mesmo valor e ganham o jogador que recebe 25 (ou mais) sementes. Sempre que houver apenas uma semente em cada jogador, os jogadores devem contar suas pedras.

O tabuleiro Ouri tem 6 compartimentos (furos) em cada lado. No início do jogo, cada um dos 12 buracos tem 4 sementes. Os dois jogadores são colocados cara a cara e colocam as sementes capturadas na mesa do lado direito. O primeiro jogador recolhe todas as sementes de um dos seus buracos e distribui-as sequencialmente através dos orifícios seguintes no sentido contrário ao dos ponteiros do relógio. Enquanto houver buracos com mais sementes, o jogador só pode tocar aqueles com uma semente. Quando a última semente é depositada na casa de um oponente, ela contém dois ou três, e estes podem ser pegos. Você se aposenta e é salvo no lado direito da mesa. Sempre que as casas tiverem duas ou três sementes antes da última e pertencerem ao oponente, elas podem e devem ser apanhadas até que seja encontrada uma casa que não preencha nenhuma dessas condições.
Quando a última semente é colocada na casa do adversário, ela contém 4 ou mais sementes, contando qual semente será descartada. Passe o jogo para o adversário. Se o jogador for sem cor em um turno, o oponente deve fazer um movimento que traz sementes para o seu lado. Quando um jogador recolhe mais sementes (25 ou mais), o jogo acaba e o jogador ganha.
Cubo de Rubik (Cubo Mágico)
O Cubo de Rubik (mais conhecido no Brasil como Cubo Mágico) é um quebra-cabeça de rotação, criado em 1974 pelo engenheiro civil e arquiteto hungaro Erno Rubik. Em 1980 o cubo conquistou prêmio especial de Melhor jogo de paciência. Tal jogo gozou de grande popularidade, especialmente no início dos anos 80.
Um cubo de tamanho padrão é um cubo com um comprimento de borda de 57 mm medido nos eixos centrais. No entanto, também existem variantes maiores ou menores, como com um comprimento de borda de 54,4 mm. O cubo é dividido em altura, largura e profundidade em três camadas, que podem ser trazidas para coincidir por rotações de 90 graus em torno de seus respectivos eixos espaciais. Como resultado, a posição e a posição de 20 do total de 26 pedras podem ser alteradas quase arbitrariamente.

Nas superfícies exteriormente visíveis das pedras são coladas pequenas áreas de cor ou as próprias pedras são coloridas. Na posição básica, as pedras são dispostas de tal maneira que cada lado do cubo tem uma cor uniforme mas diferente de lado a lado. O cubo padrão é preto na cor base e as cores dos rostos são branco versus amarelo, azul em frente a verde e vermelho em frente a laranja. A orientação das cores ao visualizar a pedra do canto branco-azul-vermelho corresponde ao topo branco, direito azul e vermelho à esquerda. Para um cubo na cor base branca, a área branca é frequentemente substituída por uma preta.
O objetivo é geralmente retornar o cubo à sua posição básica depois de virar as páginas para uma posição aleatória. À primeira vista, essa tarefa parece extremamente difícil, mas as estratégias foram desenvolvidas desde o início, cujo conhecimento permite uma solução relativamente fácil.
Tangram
Tangram é um antigo jogo de estratégica chinês, provavelmente criado entre os séculos VIII e IV aC. O nome ocidental do jogo de paciência parece ser uma expressão idiomática que pode ter apelo à dinastia Tang chinesa.
Depois que os primeiros livros originais foram impressos na China no início do século 19, o jogo foi distribuído por volta de 1813 na Europa e na América. O jogo experimentou um renascimento em meados da década de 1970, quando a editora DuMont publicou um livro combinado em brochura em bilingue alemão / holandês em 1976, no qual cerca de 1.600 modelos foram listados.
Segundo a lenda, um monge uma vez instruiu seu aluno a viajar para pintar a essência da beleza diversificada do mundo em uma telha cerâmica. Infelizmente, o tablet quebrou em sete partes diferentes e o estudante não podia mais dobrá-las em um quadrado. Ele tentou por dias. Um número infinito de padrões e imagens foi criado.

No final, o aluno entendeu: ele não precisa viajar para o mundo. Ele pode facilmente redescobrir a beleza e a diversidade do mundo nas sete partes da tabuinha quebrada.
O jogo consiste em sete peças em formas geométricas simples. Os azulejos são feitos “cortando” um quadrado em dois triângulos grandes, um triângulo de tamanho médio, dois pequenos triângulos, um quadrado e um paralelogramo.
Inúmeras formas podem ser criadas a partir dessas peças, que então mostram animais, navios ou outras formas semelhantes a silhuetas. Normalmente, todas as partes devem ser usadas e não devem ser sobrepostas.