Função do 1º Grau [Matemática]

Um grau em uma função polinomial é o maior expoente dessa equação, que determina o maior número de soluções que uma função poderia ter e o maior número de vezes que uma função cruzará o eixo x quando representada graficamente.

Cada equação contém de um a vários termos, divididos por números ou variáveis ​​com expoentes diferentes. Por exemplo, a equação y =  4 x ¹³ + 6 x ³  tem dois termos, 4x ¹³ e 6x ³  e o grau do polinômio é 13, pois esse é o grau mais alto de qualquer termo na equação.

Em alguns casos, a equação polinomial deve ser simplificada antes que o grau seja descoberto, se a equação não estiver na forma padrão. Esses graus podem então ser usados ​​para determinar o tipo de função que essas equações representam: linear, quadrática, cúbica, quártica e similares.

O exame das funções é importante, uma vez que estão sob diferentes circunstâncias podem ser aplicadas: no cálculo técnico de animais ameaçados, etc. O significado da função é inerente à matemática e permanece o mesmo para todo tipo de função, seja na 1ª ou na 2ª classe ou em uma função exponencial ou logarítmica. Portanto, a função é usada para unir valores numéricos de uma determinada expressão algébrica de acordo com cada valor que a variável x assume. Assim, a função do 1º grau refere-se aos valores numéricos obtidos a partir de expressões algébricas do tipo (ax + b) e assim forma a função f (x) = ax + b.

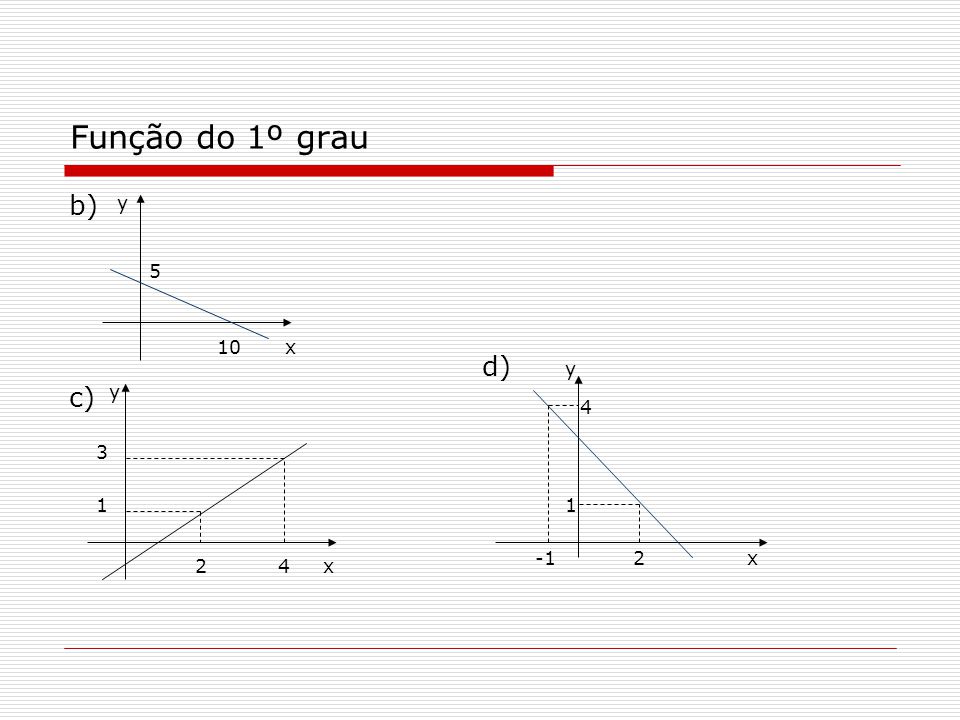
Considere x e y como duas variáveis, uma dependendo da outra, ou seja, para cada valor atribuído a x, isso é igual a um valor para y. Nós definimos essa dependência como uma função, onde y é uma função de x. O conjunto de valores dado a x deve ser chamado de domínio da função e os valores de y são a imagem da função. Cada função é definida por uma lei da educação, no caso de uma função de primeiro grau, a lei da formação é a seguinte: y = ax + b, onde a e b são números reais e a ≠ 0. Esse tipo de função tem que ser do real para o real. A representação gráfica de uma função de 1º grau é uma linha reta. Na análise da lei de formação y = ax + b, determinamos a dependência entre x e y e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função está aumentando ou diminuindo, e o valor de b mostra a interseção da função com o eixo y no plano cartesiano.

Gráfico da função

O gráfico é a representação de todos os pontos que pertencem a uma função do primeiro grau no plano. Como a função do primeiro grau é linear, seu gráfico sempre será uma reta.

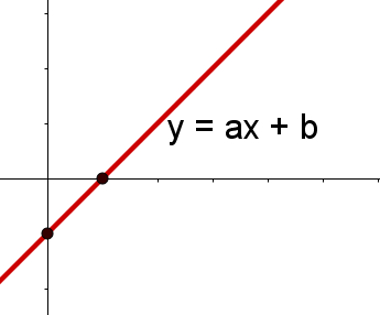
Para construí-lo, devemos lembrar um dos postulados da geometria: existe uma única linha, os dois diferentes

e contém pontos que pertencem ao nível.

Se você usar este postulado, você só precisa encontrar a posição de dois pontos no plano para construir a linha que o contém. O método utilizado depende da lei da formação de funções de primeira ordem e é apresentado em etapas:

1 – escolha dois valores para x;

2 – Substitua esses valores na função.

3 – Encontre os valores y apropriados.

Então o valor escolhido para x e seu y correspondente formam um par ordenado que pode ser marcado no nível cartesiano.

Como escolhemos dois valores para x, temos dois valores para y e, portanto, dois pares ordenados. Como sabemos que cada par ordenado é a posição de um ponto no nível cartesiano, já temos dois pontos. Apenas marque-os e desenhe a linha que passa por eles.

Existe um segundo método para criar o diagrama que contém informações importantes sobre ele e pode ser encontrado em alguns exercícios. Para usá-lo, faça o seguinte:

1 – Selecione x = 0 e substitua esse valor na função para encontrar o valor de y. Como sabemos que a função y = ax + b, temos o seguinte resultado:

y = ax + b

y = a * 0 + b

y = b

Portanto, o primeiro ponto é (0, b). Este é o ponto de encontro entre o gráfico da função e o eixo y e é sempre dado pelo coeficiente b da função de primeiro grau.

2 – Selecione y = 0 e substitua esse valor na função para obter o valor do x correspondente. Se sabemos que a função do primeiro grau é y = ax + b, temos:

y = ax + b

0 = ax + b

ax = – b

x = b
a

Portanto, o segundo ponto é (-b / a, 0). Esta é a raiz da função do primeiro grau, isto é, do ponto de encontro entre o gráfico e o eixo x.

Essas duas etapas nos fornecem as coordenadas de dois pontos pertencentes ao gráfico da função. Para construí-lo, basta desenhar a linha que passa por ele.

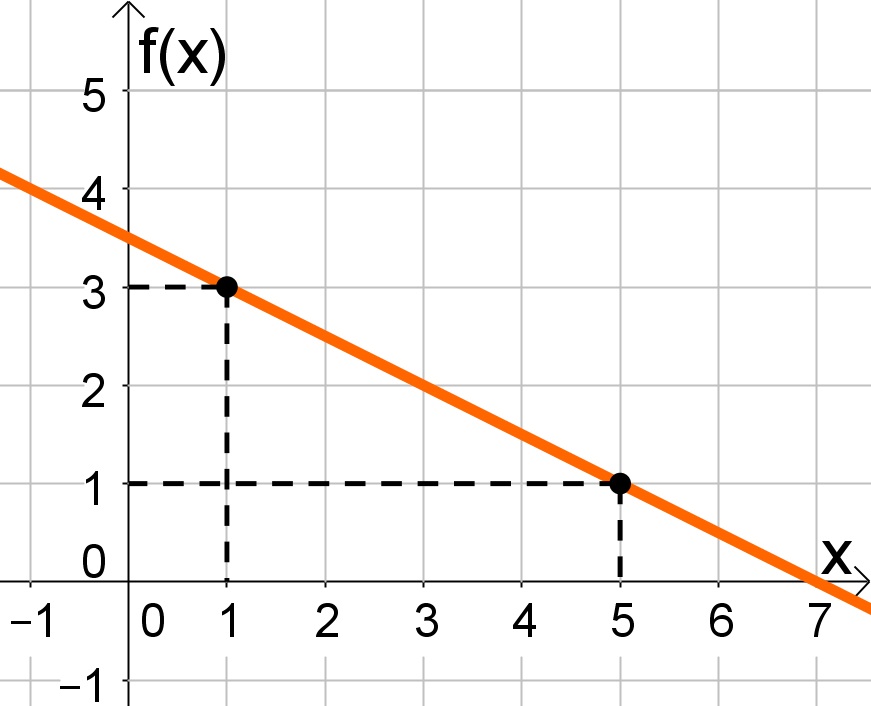
Nomes de Graus Polinomiais

Descobrir qual o grau polinomial que cada função representa ajudará os matemáticos a determinar que tipo de função ele está lidando, pois cada nome de grau resulta em uma forma diferente quando representado graficamente, começando com o caso especial do polinômio com zero grau. Os outros graus são os seguintes:

• Grau 0: uma constante diferente de zero
• Grau 1: uma função linear
• Grau 2: quadrático
• Grau 3: cúbico
• Grau 4: quártico ou biquadrático
• Grau 5: quíntico
• Grau 6: sêxtico
• Grau 7: séptico

Grau polinomial maior que o Grau 7 não foi devidamente nomeado devido à raridade de seu uso, mas o Grau 8 pode ser declarado como oceico, Grau 9 como nonico e Grau 10 como decico.

Os graus polinomiais de nomeação ajudarão os alunos e professores a determinar o número de soluções para a equação, além de reconhecer como eles funcionam em um gráfico.

O grau de uma função determina o maior número de soluções que a função pode ter e o maior número de vezes que uma função cruzará o eixo x. Como resultado, às vezes o grau pode ser 0, o que significa que a equação não possui nenhuma solução ou nenhuma instância do gráfico cruzando o eixo x. 

Nesses casos, o grau do polinômio é deixado indefinido ou é declarado como um número negativo, como negativo ou infinito negativo, para expressar o valor de zero. Esse valor é geralmente chamado de polinômio zero.

Nos três exemplos seguintes, pode-se ver como esses graus polinomiais são determinados com base nos termos de uma equação:

• y = x (Grau: 1; Apenas uma solução)
• y = x ² (grau: 2; duas soluções possíveis)
• y = x ³ (Grau: 3; Três soluções possíveis)

O significado desses graus é importante para perceber ao tentar nomear, calcular e representar graficamente essas funções na álgebra. Se a equação contiver duas soluções possíveis, por exemplo, saberemos que o gráfico dessa função precisará cruzar o eixo x duas vezes para que seja preciso. Por outro lado, se podemos ver o gráfico e quantas vezes o eixo x é cruzado, podemos facilmente determinar o tipo de função com a qual estamos trabalhando.