O que é Sistema de Equação?
Um sistema de equações consiste em uma série de equações que são mais do que um desconhecido. Para resolver um sistema, os valores devem ser encontrados para satisfazer simultaneamente todas as equações.
Um sistema é considerado de primeiro grau se o maior expoente do desconhecido que integra as equações for igual a 1 e não houver multiplicação entre esses desconhecidos.
Um sistema de equação de primeira ordem com dois desconhecidos é formado por duas equações, cada equação tendo duas variáveis x e y.
Observe o exemplo:
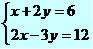
A resolução de um sistema é calcular o valor de x e y que satisfazem as equações do sistema. A solução de um sistema pode ser feita por dois métodos de resolução: adição e substituição.
Método de adições
Consiste em adicionar as variáveis semelhantes das duas equações para obter um resultado igual a zero. Veja a seguinte resolução do sistema:
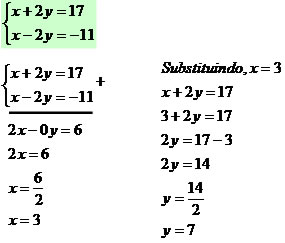
Método de substituição
Consiste em isolar x ou y em uma das equações do sistema e substituir o valor isolado na outra equação. veja:
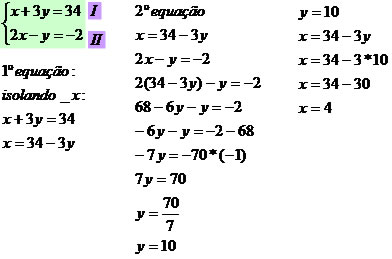
A partir dos exemplos resolvidos, podemos ver que podemos resolvê-lo usando o método de adição ou o método de substituição, dependendo da configuração do sistema.
A solução para um sistema consiste em um resultado chamado de par ordenado. O gráfico de uma equação de primeiro grau é indicado por uma linha. Em um sistema de duas equações, duas linhas retas são mostradas no plano cuja interseção é a solução geométrica do sistema. Concluímos que a solução de um sistema pode ser representada em duas formas matemáticas, uma algébrica (geométrica).

Exercícios Sobre Sistema De Equação
Questão 1
John adora animais de estimação e charadas. Um dia, um amigo perguntou-lhe quantos cães e quantos gatos ele tinha. John prontamente respondeu com o seguinte enigma: “A soma do dobro do número de cães e três vezes o número de gatos é 17. E a diferença entre o número de cães e gatos é de apenas 1”. Você pode descobrir quantos cães e quantos gatos John tem?
Resposta:
Primeiro, vamos interpretar o enigma de João algebricamente. Nós identificamos o número de gatos com g e o número de cães com c. Se “a soma do dobro do número de cães e a triplicação do número de gatos for igual a 17”, chegamos a:
2 c + 3 g = 17
E se “a diferença entre o número de cães e gatos for apenas 1”, podemos concluir:
c-g = 1
Com as equações encontradas, podemos montar o seguinte sistema:
Para resolver este sistema pelo método de adição, multiplicamos todos os termos da segunda equação por 3 e adicionamos as equações:
5 c + 0 g = 20
5 · c = 20
c = 20
5
c = 4
Se usarmos c = 4 em c – g = 1, temos:
c-g = 1
4 – g = 1
– g = 1-4
(- 1) · (- g) = (- 3) · (- 1)
g = 3
Podemos concluir que John tem três gatos e quatro cachorros
Questão 2
Em sua rua, André notou que 20 motocicletas estavam estacionadas entre motocicletas e carros. Quando ele se abaixou, viu 54 rodas. Quantas bicicletas e carros existem na rua do André?
Se identificarmos o número de bicicletas com o desconhecido m e o número de carros com o desconhecido c, podemos dizer que a equação m + c = 20 é válida.
Como sabemos que cada motocicleta tem duas rodas e cada carro 4, podemos montar outra equação: 2 · m + 4 · c = 54. Se as organizarmos em um sistema de equações, temos
Para resolver este sistema pelo método de substituição, isolamos m na primeira equação e substituímos com a segunda:
m + c = 20
m = 20 – c
2m + 4c = 54
2 · (20 – c) + 4 · c = 54
40 – 2 · c + 4 · c = 54
– 2 · c + 4 · c = 54-40
2 · c = 14
c = 14
2
c = 7
Se usarmos c = 7 em m = 20 – c, temos:
m = 20 – c
m = 20-7
m = 13
A rua de André tem treze bicicletas e sete carros.
Questão 3
Um supermercado comprou detergentes de limão e coco. A compra foi entregue em 10 caixas de 24 garrafas por caixa. Como se sabia que cada caixa continha 2 garrafas de detergente mais contidas na fragrância de limão do que no cheiro de coco, o número de garrafas fornecidas na fragrância de limão era:
a) 110
b) 120
c) 130
d) 140
e) 150
Segundo o comunicado, as caixas contêm detergentes em fragrância de limão e cheiro de coco. Vamos representar suas quantidades com as variáveis L e C, respectivamente. Sabemos que terá um total de 24 produtos de limpeza pela soma das quantidades das duas essências em uma caixa, ou seja, G + C = 24. Também sabemos que cada caixa contém dois detergentes de limão a mais do que coco = C + 2. Para esta equação para reorganizar, temos: L – C = 2.
Com as equações identificadas, podemos montar um sistema que seja resolvido pelo método de adição:
2 L + 0 C = 26
2 L = 26
L = 26
2
L = 13
Cada caixa continha 13 garrafas de detergente com cheiro de limão. No entanto, como 10 caixas foram diluídas com a mesma quantidade (13 x 10 = 130), o supermercado comprou 130 garrafas de louça. A resposta correta é a letra c.
Questão 4
Em uma liga de futsal, quando um time vence, marca 3 pontos; se empates, marca um ponto e não perdeu pontos. Admito que neste campeonato, o Time A participou de 16 jogos e perdeu apenas dois jogos. Se o Time A, nestes jogos, 24 pontos, então a diferença entre o número de jogos ganhava a equipe e o número de jogos que desenhavam nessa ordem.
a) 8.
b) 4.
c) 0
d) – 4.
e) – 8.
Segundo o comunicado, a equipe participou dos 16 jogos e perdeu dois deles. Então podemos dizer que em 14 jogos, o time ganhou ou empatou. Representando a letra v jogos em que a equipe venceu e daqueles que vieram, nós algébricos v + e = 14 (o número de vitórias sorteadas mais o número igual a 14). Para determinar a pontuação de uma equipe, multiplique por 3 e escolha 1 e adicionamos os resultados. No caso do Time A, temos:
3 · v + 1 · e = 24
3 · v + e = 24
Podemos montar o seguinte sistema de equação:
Vamos resolver este sistema com o método de substituição. Pois o desconhecido e a primeira equação são sempre isolados: e = 14 – v. Se substituirmos este valor de e na segunda equação, temos:
3 · v + e = 24
3 · v + 14 – v = 24
3 · v – v = 24 – 14
2 · v = 10
v = 10
2
v = 5
Se usarmos o valor encontrado de v em e = 14 – v, temos:
e = 14 – v
e = 14-5
e = 9
A equipe A teve nove empates e cinco vitórias, mas o exercício pediu a diferença entre o número de jogos em que o won e o número de partidas em que equilibrou. Essa diferença é 5 – 9 = – 4. A alternativa correta é a letra d.


