
Trigonometria é o estudo das relações entre ângulos e lados de um triângulo. Para um triângulo retângulo definimos as razões: seno, cosseno e tangente.
As razões são úteis para resolver problemas onde precisamos descobrir um lado e conhecer a medida de um ângulo, além do ângulo reto e um dos seus lados.
Exercícios sobre seno, cosseno e tangente de ângulos podem ser resolvidos aplicando os ângulos notáveis.
Exercício 1
Um avião decola, percorrendo uma trajetória retilínea, formando com o solo um ângulo de 30° (suponha que a região sobrevoada pelo avião seja plana). Depois de percorrer 1.000 metros, a altura atingida pelo avião, em metros, é:
Resposta
Interpretando a situação descrita no problema, temos a seguinte imagem que ilustra a situação em que a altura atingida pelo avião é dada por x:
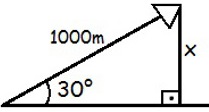
Utilizando a fórmula para o cálculo do seno, temos:
Portanto, o avião atingiu 500 m de altura.
Exercício 2
Determine os valores de x, y, w e z em cada caso:
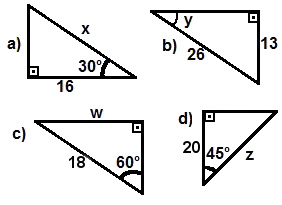
a) Através do cosseno de 30°, temos:

b) Através do seno de y:

c) Pelo seno de 60°:

d) Através do cosseno de 45°:

Exercício 3
A figura abaixo representa um avião que decolou sob um ângulo constante de 40º e percorreu em linha reta 8000 m. Nesta situação, qual a altura que se encontrava o avião ao percorrer essa distância?
Considere:
sen 40º = 0,64
cos 40º = 0,77
tg 40º = 0,84
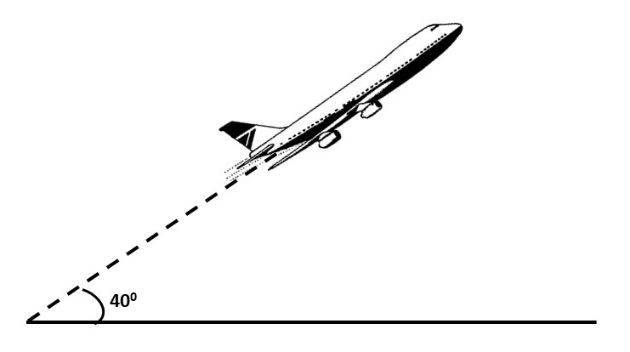
Resposta
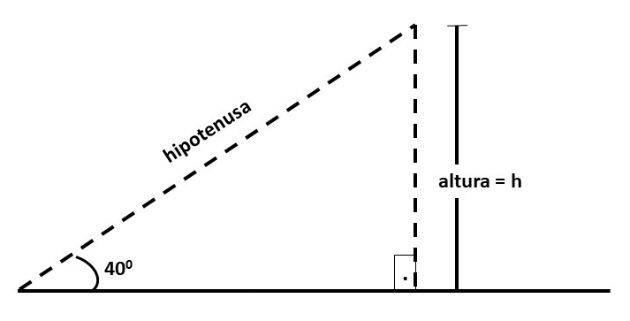
Notamos que o triângulo indicado é retângulo e a distância percorrida representa a medida da hipotenusa deste triângulo e a altura do cateto oposto ao ângulo dado.
Portanto, usaremos o seno do ângulo para encontrar a medida da altura:

Assim, ao percorrer 8 000 m, o avião se encontra a 5 120 m de altura.
Exercício 4
Uma escada que mede 6m está apoiada em uma parede. Sabendo-se que ela forma com o solo um ângulo α e que
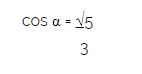
a distância de seu ponto de apoio no solo até a parede, em metros, é:
Resposta
Podemos ilustrar a situação descrita pelo enunciado do problema com a seguinte figura:
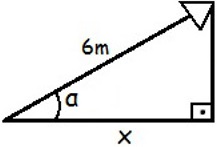
Utilizando a fórmula para o cálculo do cosseno, temos:
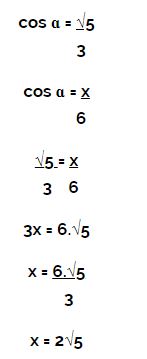
A distância do ponto de apoio até a parede é de aproximadamente 2√5 metros.
Exercício 5
Determine os ângulos agudos de um triângulo retângulo de catetos que medem √3 cm e 1 cm.
Resposta
Sejam os ângulos procurados a e b, temos então:
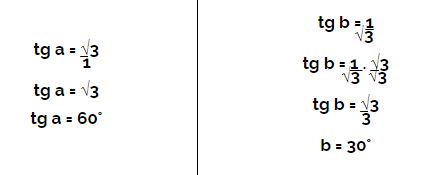
Os ângulos agudos procurados são 30° e 60°.
Exercício 6
Quando o Sol se encontra a 45º acima do horizonte, uma árvore projeta sua sombra no chão com o comprimento de 15 m. Determine a altura dessa árvore:
Resposta
Para entender melhor a questão, é adequado tentar visualizar a situação do exercício. No desenho abaixo, o segmento de reta amarelo representa um raio solar que é o responsável por originar a sombra da árvore.
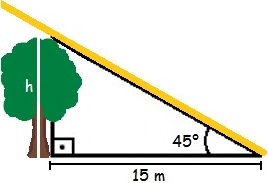
Há um ângulo de 45° com o solo, e o comprimento da sombra é a base do triângulo. Pela tabela trigonométrica dos ângulos notáveis, verificamos que a tangente de 45° é 1. Utilizando a fórmula da tangente, temos:
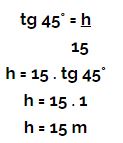
Portanto, a altura dessa árvore é de 15 metros.
Exercício 7
Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de:
a) 6√3 m.
b) 12 m.
c) 13,6 m.
d) 9√3 m.
e) 18 m.
Resposta
Podemos representar no triângulo ilustrado a seguir a situação descrita no problema. A hipotenusa representa a rampa percorrida pela pessoa citada:
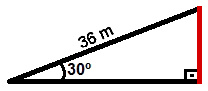
Na figura, a altura que a pessoa foi elevada está representada pelo lado vermelho (cateto oposto ao ângulo de 30°). Vamos chamar esse lado do triângulo de x para determinar seu valor. Para tanto, utilizaremos a fórmula do seno:

Portanto, ao subir a rampa, a pessoa eleva-se verticalmente 18 m. Logo, a alternativa correta é a letra e.
Exercício 8
Se um cateto e a hipotenusa de um triângulo retângulo medem 2a e 4a, respectivamente, então a tangente do ângulo oposto ao menor lado é:
a) 2√3
b) √3
3
c) √3
6
d) √20
20
e) 3√3
Resposta
Exercício 9
Para uma feira de ciências um grupo de estudantes resolveu construir uma maquete de uma casa, conforme esquema abaixo. O telhado será feito com uma placa de isopor de 1m de comprimento, que será dividida ao meio para fazer as duas partes do telhado. Sabendo que o telhado será feito segundo um ângulo de 55º, calcule a medida x da largura casa.
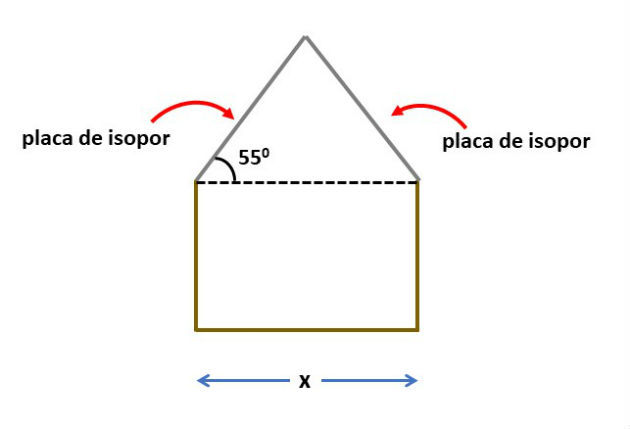
Considere:
sen 55º = 0,82
cos 55º = 0,57
tg 55º = 1,43
Como o telhado da maquete será feito com uma placa de isopor de 1m de comprimento, ao dividir a placa ao meio, a medida de cada lado do telhado será igual a 0,5 m.
O ângulo de 55º é o ângulo formado entre a reta que representa o telhado e uma reta na direção horizontal. Se unirmos essas retas, formamos um triângulo isósceles (dois lados de mesma medida).
Vamos então traçar a altura deste triângulo. Como o triângulo é isósceles, essa altura divide a sua base em segmentos de mesma medida que chamamos de y, conforme figura abaixo:
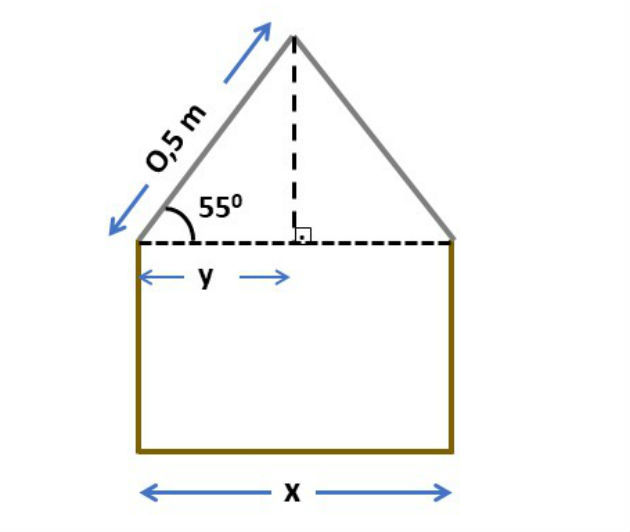
A medida y será igual a metade da medida de x, que corresponde a largura da casa.
Desta forma, temos a medida da hipotenusa do triângulo retângulo e procuramos a medida de y, que é o cateto adjacente ao ângulo dado.
Assim, podemos usar o cosseno de 55º para calcular esse valor:

Como a largura da casa é igual a duas vezes essa medida, então temos:
largura da casa = 2. 0,285 = 0,57
Assim, a maquete da casa terá uma largura de 0,57 m ou 57 cm.
Exercício 10
Um menino avista o ponto mais alto de um morro, conforme figura abaixo. Considerando que ele está a uma distância de 500 m da base do morro, calcule a altura (h) deste ponto.
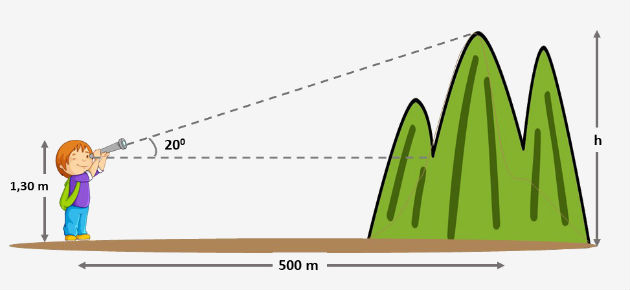
Considere:
sen 20º = 0,34
cos 20º = 0,93
tg 20º = 0,36
Resposta
Observando o desenho, notamos que o ângulo visual é de 20º. Para calcular a altura do morro, iremos usar as relações do seguinte triângulo:
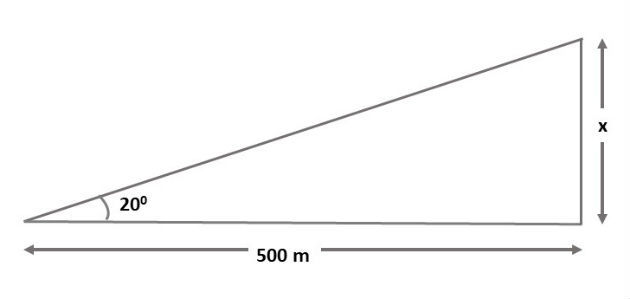
Como o triângulo é retângulo, iremos calcular a medida x usando a razão trigonométrica tangente.
Escolhemos essa razão, visto que conhecemos o valor do ângulo do cateto adjacente e estamos procurando a medida do cateto oposto (x).
Assim, teremos:
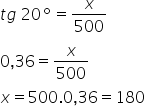
Como o menino tem 1,30 m, a altura do morro será encontrada somando-se este valor ao valor encontrado para x. Assim, teremos:
h = 180 + 1,3 =181,3
Logo, a altura do morro será igual a 181,3 m.
O que você achou dos exercícios? Deixe a sua opinião nos comentários! E também vote nas estrelinha a baixo.


