
Vamos praticar exercícios de função do 1º grau!
é importante verificar se a função é crescente ou decrescente, bem como os zeros da função.
Exercício 1
Determine os zeros das funções a seguir:
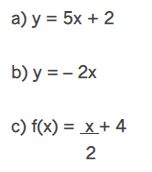
Resposta

Exercício 2
Determine a função afim f(x) = ax + b, sabendo que f(1) = 5 e f(–3) = –7.
Resposta
f(1) = 5
f(1) = a * 1 + b
5 = a + b
a + b = 5
f(–3) = –7
f(–3) = a * (–3) + b
f(–3) = –3a + b
–3a + b = –7
Sistema de equações

Isolando a na 1º equação
a + b = 5
a = 5 – b
Substituindo o valor de a na 2º equação
–3a + b = –7
–3 * (5 – b) + b = –7
–15 + 3b + b = –7
4b = –7 + 15
4b = 8
b = 2
Substituindo o valor de b na 1º equação
a = 5 – b
a = 5 – 2
a = 3
A função será definida pela seguinte lei de formação: f(x) = 3x + 2.
Exercício 3
Classifique cada uma das funções seguintes em crescente ou decrescente:
a) y = 4x + 6
b) f(x) = – x + 10
c) y = (x + 2)2 – (x – 1)2
Resposta
Em uma função do tipo y = ax + b, o coeficiente a de x indica se a função é crescente ou decrescente.
a) y = 4x + 6
Nessa função, a = 4 > 0, portanto, y é uma função crescente.
b) f(x) = – x + 10
Como a = – 1 < 0, f(x) é uma função decrescente.
c) y = (x + 2)2 – (x – 1)2
Nesse caso precisamos desenvolver os parênteses através dos produtos notáveis.
x2 + 4x + 4 – (x – 1)2
x2 + 4x + 4 – (x2 – 2x + 1)
x2 + 4x + 4 – x2 + 2x – 1
6x + 3
y = 6x + 3. Como a = 6 > 0, y é uma função crescente.
Exercício 4
Seja a função f de R em R definida por f(x) = 54x + 45, determine o valor de f(2 541) – f(2 540).
Resposta
f(2 541) = 54 * 2 541 + 45
f(2 541) = 137 214 + 45
f(2 541) = 137 259
f(2 540) = 54 * 2 540 + 45
f(2 540) = 137 160 + 45
f(2 540) = 137 205
f(2 541) – f(2 540) → 137 259 – 137 205 → 54
A diferença será igual a 54.
Exercício 5
O gráfico da função f (x) = mx + n passa pelos pontos (– 1, 3) e (2, 7). O valor de m é:
a) 5/3
b) 4/3
c) 1
d) 3/4
e) 3/5
O primeiro ponto que é dado é o (– 1, 3), em que o valor de x é – 1 e o valor de f(x) é 3. Substituindo esses valores na função, temos:
f (x) = mx + n
3 = m.(– 1) + n
n = 3 + m
Vamos também substituir o segundo ponto (2, 7) na função, sendo que x vale 2e f(x) vale 7:
f (x) = mx + n
7 = m.2 + n
n = 7 – 2m
Nas duas substituições feitas, encontramos dois valores para n. Se igualarmos essas duas equações, teremos:
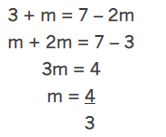
A alternativa correta é a letra b.
Exercício 6
Uma função f é dada por f(x) = ax + b, em que a e b são números reais. Se f(–1) = 3 e f(1) = –1, determine o valor de f(3).
Resposta
f(x) = ax + b
f(–1) = 3
f(–1) = a * (–1) + b
3 = – a + b
f(1) = –1
f(1) = a * 1 + b
–1 = a + b
Sistema de equações
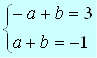
Isolando b na 1ª equação
–a + b = 3
b = 3 + a
Substituindo o valor de b na 2ª equação
a + b = –1
a + 3 + a = –1
2a = –1 – 3
2a = –4
a = – 2
Substituindo o valor de a na 1ª equação
b = 3 + a
b = 3 – 2
b = 1
A função será dada pela expressão f(x) = – 2x + 1. O valor f(3) será igual a:
f(3) = –2 * 3 + 1
f(3) = – 6 + 1
f(3) = – 5
O valor de f(3) na função f(x) = – 2x + 1 é igual a –5.
Exercício 7
A função R(t) = at + b expressa o rendimento R, em milhares de reais, de certa aplicação. O tempo t é contado em meses, R(1) = –1 e R(2) = 1. Nessas condições, determine o rendimento obtido nessa aplicação, em quatro meses.
Resposta
R(1) = –1
R(1) = a * 1 + b
–1 = a + b
a + b = –1
R(2) = 1
R(2) = a * 2 + b
1 = 2a + b
2a + b = 1
Sistema de equações
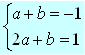
Isolando b na 1ª equação
a + b = –1
b = –1 – a
Substituindo o valor de b na 2ª equação
2a + b = 1
2a + (–1 – a) = 1
2a – 1 – a = 1
a = 1 + 1
a = 2
Substituindo o valor de a na 1ª equação
b = – 1 – a
b = –1 – 2
b = –3
A função será dada pela seguinte lei de formação: R(t) = 2t – 3.
Fazendo f(4), temos:
R(t) = 2 * 4 – 3
R(t) = 8 – 3
R(t) = 5
O rendimento obtido nessa aplicação será de R$ 5 000,00.
O que você achou dos exercícios? Conseguiu resolvê-los? Deixe o seu comentário e vote nas estrelinhas!


