Para resolver os exercícios sobre equação exponencial, procure encontrar uma igualdade entre as potências de mesma base para que se igualem também os expoentes.
Exercício 1
Determine o conjunto solução da seguinte equação exponencial:
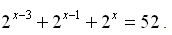
Resposta
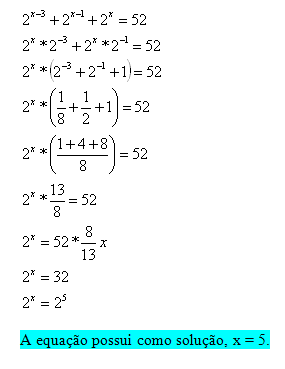
Exercício 2
Resolva a equação exponencial:
– 5x – 1 – 5x + 5x + 2 = 119
Resposta
Como temos na equação a adição e a subtração de potências, não podemos escrever o primeiro membro como uma só potência, mas podemos desmembrar as potências na maior quantidade possível. Isso corresponde a escrever a equação da seguinte forma:
– 5x – 1 – 5x + 5x + 2 =
– 5x · 5– 1 – 5x + 5x · 52 =
Colocando o termo 5xem evidência, temos:
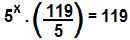
Portanto, a solução da equação exponencial – 5x – 1 – 5x + 5x + 2 = 119 é x = 1.
Exercício 3
Qual o valor de x na equação exponencial
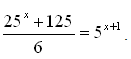
Resposta
Exercício 4
Dada a equação 23x – 2 · 8x + 1 = 4x – 1, podemos afirmar que sua solução é um número:
a) natural.
b) maior do que 1.
c) de módulo maior do que 1.
d) par.
e) de módulo menor do que 1.
Resposta
A fim de facilitar a resolução da equação exponencial 23x – 2 · 8x + 1 = 4x – 1, vamos reescrever todas as potências na base 2. A saber, temos: 4 = 22e 8 = 23. Substituindo na equação:
23x – 2 · 8x + 1 = 4x – 1
23x – 2 · (23)x + 1 = (22)x – 1
23x – 2 · 23(x + 1) = 22(x – 1)
23x – 2 · 23x + 3 = 22x – 2
2(3x – 2 ) + (3x + 3) = 22x – 2
Como temos uma equação exponencial que apresenta potências de mesma base nos dois lados da equação, podemos igualar os expoentes:
(3x – 2) + (3x + 3) = 2x – 2
6x + 1 = 2x – 2
6x – 2x = – 2 – 1
4x = – 3
x = – 3
4
|x| = ¾
Portanto, a alternativa que classifica corretamente o resultado da equação é a letra e, que afirma que x é um número de módulo menor do que 1.
Exercício 5
A soma das raízes da equação 22x + 1 – 2x + 4 = 2x + 2 – 32 é:
a) 2
b) 3
c) 4
d) 6
e) 7
Resposta
Para resolver a equação exponencial 22x + 1 – 2x + 4 = 2x + 2 – 32, começaremos separando as potências que apresentam somas no expoente, escrevendo-as como produto de potências.
22x + 1 –2x + 4= 2x + 2– 32
2x · 2x · 21– 2x · 24 = 2x · 22 – 32
Façamos 2x = y:
y · y · 21– y · 24 = y · 22 – 32
y2 · 21–y · 16=y · 4– 32
2y2–16y – 4y + 32 = 0
2y2 – 20y + 32 = 0
Chegamos a uma equação do 2° grau, que pode ser resolvida fórmula de Bhaskara. A fim de trabalhar com números menores, podemos dividir toda a equação por 2, sem prejuízo no resultado final.
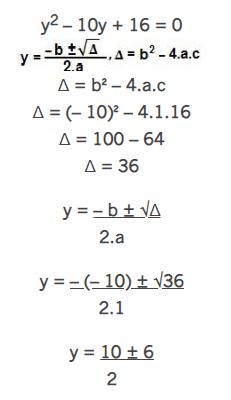
| y1 = 10 + 6 2y1 = 16 2y1 = 8 | y2 = 10 – 6 2y2 = 4 2y2 = 2 |
Agora que encontramos os possíveis valores de y, podemos resolver a equação exponencial que criamos no início do exercício:
| Para y1 = 82x = y 2x = 8 2x = 23 x1 = 3 | Para y2 = 22x = y 2x = 2 2x = 21 x2 = 1 |
O enunciado pediu a soma das raízes da equação exponencial. Como as raízes são x1 = 3 e x2 = 1, então a soma é x1 + x2 = 3 + 1 = 4. Portanto, a alternativa correta é a letra c.
O que você achou dos exercícios? Deixe o seu comentário com sua opinião! Vote nas estrelinhas para melhorar nosso conteúdo cada vez mais 🙂