
Fizemos aqui uma seleção de diversos exercícios de matemática, dos mais diversos níveis e graus de complexidade. Confira!
Exercícios de Equações do 1º Grau
Função Quadrática ou Função do 2º Grau
Exercício Sobre Função Do 1º Grau
Ao resolver exercícios sobre funções do 1º grau, é importante verificar se a função é crescente ou decrescente, bem como os zeros da função.
Questão 1
Determine os zeros das funções a seguir:
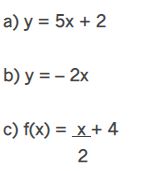
Resposta

Exercício Sobre Progressões
Para resolver exercícios sobre progressões, devemos aplicar as fórmulas do termo geral e da soma dos termos de uma PA e de uma PG.
Encontre o termo geralda progressão aritmética (PA) abaixo:
A = (3, 7, …)
Resposta
Apesar de a sequência apresentar apenas dois elementos, já podemos destacar dois termos importantes. Temos o primeiro elemento (a1 = 3) e ainda a razão, que é dada pela diferença de um termo pelo termo imediatamente anterior. Portanto, a razão r é dada por r = 7 – 3 = 4. Dessa forma, é possível determinar a fórmula de seu termo geral:
an = a1 + (n – 1).r
an = 3 + (n – 1).4
an = 3 + 4n – 4
an = 4n – 1
Então, o termo geral da PA (3, 7, …) é an = 4n – 1.
Exercício Sobre Equação Biquadrada
É possível resolver exercícios sobre equação biquadrada convertendo-a em uma equação polinomial do segundo grau.
O conjunto solução, no campo real, da equação z4 – 13z2 + 36 = 0 é:
a) S = {-3, -2, 0, 2, 3}
b) S = {-3, -2, 2, 3}
c) S = {-2, -3}
d) S = {0, 2, 3}
e) S = {2, 3}
Resposta


Exercício Sobre Equação Do 2° Grau
Através da fórmula de Bhaskara, conseguimos resolver exercícios sobre equação do 2º grau.
Resolva a equação: 4x2 + 8x + 6 = 0
Resposta
Os coeficientes da equação são: a = 4, b = 8, c = 6. Substituindo esses valores na fórmula de Bhaskara, temos:

Exercício Sobre Notação Especial Da Progressão Aritmética
Ao resolvermos exercícios sobre notação especial da progressão aritmética, devemos atentar para o fato de os termos da PA serem desconhecidos.
A sequência de números positivos (x, x + 10, x², …) é uma PA, cujo 10° termo é:
a) 94
b) 95
c) 101
d) 104
e) 105
Resposta
Primeiramente, se estamos lidando com uma progressão aritmética, sabemos que a diferença de um termo com o elemento imediatamente anterior resulta na razão dessa progressão. Logo:

O valor de x2 = – 4 não é interessante nesse problema, pois os elementos dessa sequência são positivos. Portanto, utilizaremos apenas x1 = 5. Sendo assim, podemos reescrever os elementos da sequência da seguinte forma:

Exercício Sobre Propriedades Das Potências
Em exercícios sobre propriedades das potências, normalmente aplicamos todas as regras de potenciação para simplificar e resolver expressões.
Simplifique a expressão:
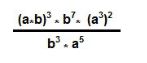
Resposta
Entre as propriedades de potenciação, vamos aplicar as propriedades da potência de um produto e da potência de potência:

Exercício Sobre Quadrado Da Soma E Quadrado Da Diferença
Utilizando conceitos de produtos notáveis e fatoração, é possível resolver exercícios sobre quadrado da soma e quadrado da diferença.
Desenvolva os seguintes produtos notáveis:
a) (x + y)2
b) (2a + b)2
c) (x – 5y)2
d) (3 – a3)2
Resposta
Podemos resolver esses produtos notáveis através da seguinte ideia:
“O primeiro termo elevado ao quadrado mais (ou menos) o dobro do primeiro termo multiplicado pelo segundo termo mais o segundo termo elevado ao quadrado.”
a) (x + y)2 = x2 + 2.x.y + y2
b) (2a + b)2 = (2a)2 + 2.2a.b + b2 = 4a2 + 4ab + b2
c) (x – 5y)2 = x2 – 2.x.5y + (5y)2 = x2 – 10xy + 25y2
d) (3 – a3)2 = 32 – 2.3.a3 + (a3)2 = 9 – 6a3 + a6
Exercício Sobre Progressão Aritmética
Estes exercícios sobre progressão aritmética são resolvidos através da fórmula do termo geral e da soma dos termos de uma PA finita.
Em relação à progressão aritmética (10, 17, 24, …), determine:
a) o termo geral dessa PA;
b) o seu 15° termo;
c) a soma a10 + a 20.
a) Para encontrar o termo geral da progressão aritmética, devemos, primeiramente, determinar a razão r:
r = a2 – a1
r = 17 – 10
r = 7
A razão é 7, e o primeiro termo da progressão (a1) é 10. Através da fórmula do termo geral da PA, temos:
an = a1 + (n – 1). r
an = 10 + (n – 1). 7
Portanto, o termo geral da progressão é dado por an = 10 + (n – 1). 7.
b) Como já encontramos a fórmula do termo geral, vamos utilizá-la para encontrar o 15° termo. Tendo em vista que n = 15, temos então:
an = 10 + (n – 1). 7
a15 = 10 + (15 – 1). 7
a15 = 10 + 14 . 7
a15 = 10 + 98
a15 = 108
O 15° termo da progressão é 108.
c) Vamos utilizar a fórmula do termo geral para identificar os elementos a10 e a20da PA:
an = 10 + (n – 1). 7
a10 = 10 + (10 – 1). 7
a10 = 10 + 9 . 7
a10 = 10 + 63
a10 = 73
an = 10 + (n – 1). 7
a20 = 10 + (20 – 1). 7
a20 = 10 + 19 . 7
a20 = 10 + 133
a20 = 143
A soma a10 + a 20é dada por:
a10 + a 20 = 73 + 143 = 216


