O que é Geometria Plana?
A geometria plana ou euclidiana é a cadeia matemática que examina as formas geométricas que não têm volume, como triângulos, retângulos, círculos.
A geometria plana foi criada por Euclides, matemático de Alexandria, explora características e tamanho de formas e utiliza fórmulas matemáticas para calcular o perímetro e a área. Esta seção tem alguns recursos que nos ajudam a entender as formas mais complexas, como: B. Conceitos para pontos, linhas, planos e ângulos.

Quais são os Conceitos de Geometria Plana?
Para entender as formas geométricas planas, alguns conceitos básicos dessa categoria de geometria devem ser conhecidos.
Ponto
O ponto é uma forma geométrica sem a definição exacta porque não tem dimensão (superfície e cumprimento zero), ou seja, ele é identificado por “que não tem partes.” É o elemento básico para a formação de outras figuras e é representado por letras minúsculas.
Retas
Linhas infinitas sem largura, que são formadas por numerosos pontos. Elas podem ser horizontais, verticais ou diagonais, e são representados por letras minúsculas do alfabeto latino. Em termos de semelhanças, eles podem ser identificados como:
• paralelas, se não tiverem ponto em comum com outra linha;
• Concorrentes quando atingem outra linha através de um ponto comum.
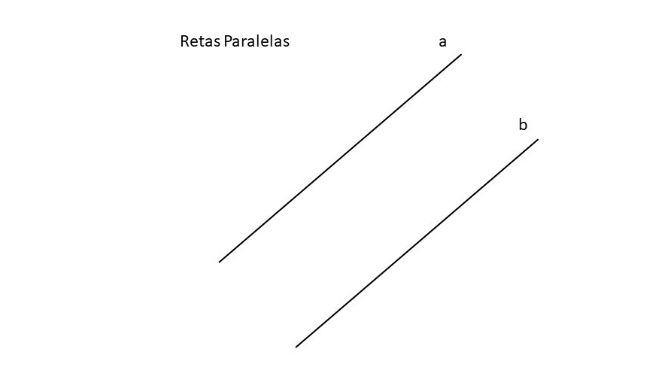
Semirretas
Linhas retas com pontos de início e fim. Ou seja, são linhas com apenas uma direção e direção, mas com uma certa origem.
Segmentos de Retas
Linhas retas divididas em dois pontos cujo tamanho é definido. Eles podem ser divididos em quatro segmentos:
• linhas consecutivas, se tiverem um ponto comum;
• linhas colineares quando dois ou mais pontos diferentes compartilham a mesma linha;
• linhas adjacentes, se permitirem pontos comuns e passarem uma linha exclusiva;
• Linhas correspondentes, se forem segmentos iguais de linhas retas.
Plano
A camada é representada pela letra minúscula do alfabeto grego (Alfa ou Beta) e consiste em um número infinito de níveis que podem seguir em todas as direções. Esta superfície tem comprimento e largura e forma a base para a formação de figuras geométricas planas.

Ângulos (Â)
Conectando dois segmentos retos a um ponto comum e graus de abertura. Eles podem ser classificados de cinco maneiras diferentes.
• zero (0 °) quando os semicírculos estão na mesma direção e se sobrepõem, sem abrir;
• afiada quando a abertura muda entre 0 ° e 90 °;
• em linha reta, se tiver um ângulo de 90 °
• sem corte se o ângulo for maior que 90 ° e menor que 180 °;
• Plana, quando as meias ondas saem em direções diferentes e formam um ângulo de 180 °.
Além destes, eles podem ser complementares se a soma dos ângulos for igual a 90 °, além disso – se a soma for igual a 180 ° – ou oposta ao vértice, se eles tiverem a mesma medida, mas apenas de um lado .
Área (s)
É todo o tamanho da superfície. Quanto maior a área de uma figura, maior a área. Ilustrado nas figuras pela letra S, é importante enfatizar que cada figura geométrica pode ser calculada a partir de certas fórmulas matemáticas.
Perímetro (P)
Resultado da soma dos comprimentos, d. H. A soma de todos os lados das formas geométricas, regulares ou não.
Figuras Geométricas Planas
Os números planares são áreas que são fechadas por segmentos de linha (pelo menos três segmentos). Como vimos, todas as formas geométricas consideradas planas possuem fórmulas matemáticas específicas para perímetro e área, uma vez que não possuem volume.
Além disso, eles podem ser classificados em: polígonos, não polígonos.
Polígonos: são segmentos de uma linha com um determinado número de lados.
Não polígonos: são figuras que podem ser abertas ou fechadas.

Triângulos
Os triângulos são polígonos com três lados (a soma dos ângulos internos será sempre de 180 °). Eles são detectados pelo número de páginas ou ângulos.
triângulo equilátero: todos os lados e ângulos internos correspondem a 60 °;
triângulo isósceles: apenas dois lados e dois ângulos internos são congruentes (iguais);
Triângulo escaleno: tem todos os lados e diferentes ângulos internos.
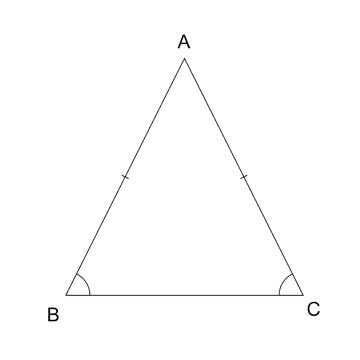
Quanto aos ângulos:
Triângulo retângulo: possui um ângulo interno de 90 ° (reto);
Triângulo Obtusângulo: tem dois ângulos agudos, ou seja, menos de 90 °;
Triângulo Acutângulo: possui três ângulos internos menores que 90 °.
Quadrado
O polígono com quatro lados iguais é o quadrado das formas geométricas que ocorrem no grupo de quadrados. Também possui quatro ângulos retos ou congruentes (90 °).
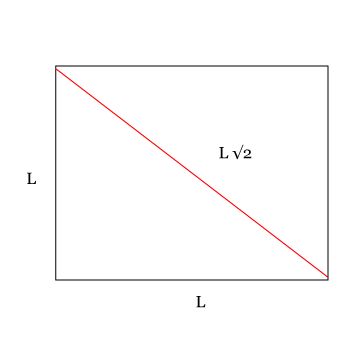
Retângulo
Cada paralelogramo tem todos os ângulos retos (90 °). Os lados opostos (vertical e horizontal) são paralelos e do mesmo tamanho.
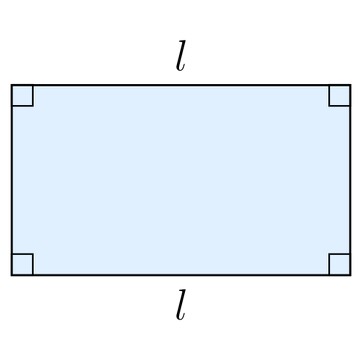
Paralelogramos são formas quadrilaterais cujos lados opostos são paralelos. Em todos os lados opostos e os ângulos são congruentes, a soma de dois ângulos sucessivos é de 180º e as diagonais são divididas em duas.
Trapézio
É um notável quadrilátero, já que a soma dos ângulos internos atinge 360 °. Tem dois lados opostos e bases paralelas, uma maior que a outra.
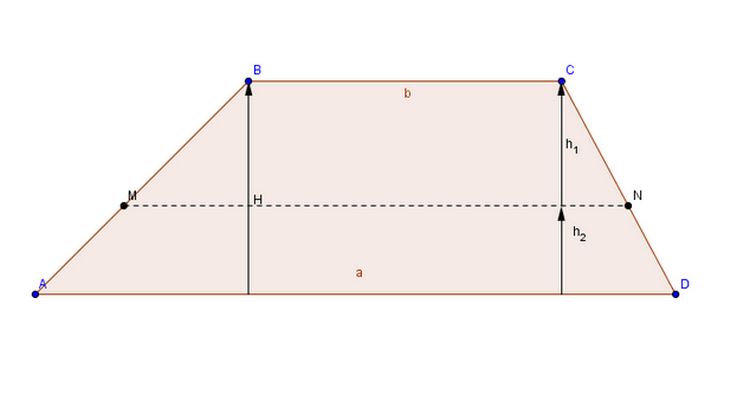
Como triângulos, eles têm classificações diferentes:
Trapézio retângulo: aqueles que têm dois ângulos de 90 ° porque um dos pontos de suas diagonais é perpendicular às bases;
Trapézio isósceles: aqueles cujos lados não paralelos têm a mesma dimensão;
Trapézio Escaleno: todos de tamanhos diferentes.
Losango
Outro tipo de quadrângulo é o diamante construído em quatro lados iguais. Suas diagonais paralelas formam o ângulo de 90 °.

O diamante pertence à classe de paralelogramos, bem como aos retângulos.
Círculo
Ao contrário dos outros polígonos, o círculo abrange todos os pontos de um plano. Seus principais componentes são o raio (r) e o ponto central.
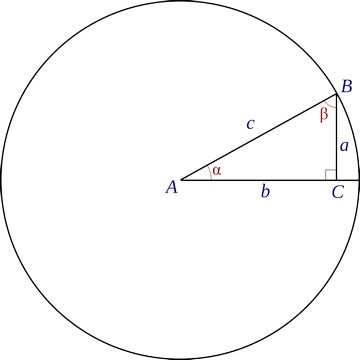
O raio é o valor da distância entre o centro do círculo e seu contorno.
Figuras não planas
Figuras não planares também são referidas como corpos geométricos e possuem largura, altura e comprimento. Como formas planas, dividem-se em duas situações: poliedros e não poliedros.
Poliedros: são corpos delimitados por uma série de superfícies. As superfícies são superfícies planas com um certo número de lados. O encontro de mão dupla é chamado de borda e o ponto de união entre múltiplas arestas é chamado de vértice do poliedro.
Sem poliedros: Também definidos como corpos redondos, os não-poliedros possuem bases arredondadas. O cilindro, a esfera e o cone são exemplos de não-polígonos.
Fórmulas de Geometria Plana
Cada figura plana mostra seu próprio cálculo matemático. Vamos para eles.
Triângulo
Para calcular a área de um retângulo triangular (ângulo de 90 °), divida o valor da multiplicação da base (b) pela altura (h) por 2. A fórmula é, portanto, A = b.h / 2.
Para triângulos equiláteros (todos os lados iguais e ângulo interno igual a 60 °), o cálculo padrão é:
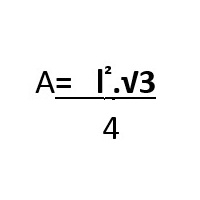
Para triângulos com ângulos menores que 90 °, os termos seno e cosseno ou meia circunferência são usados.
Retângulo
A fórmula para encontrar a antena de um retângulo é uma das mais simples da geometria plana. É a multiplicação da base com a altura, ou seja:
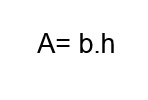
Quadrado
É basicamente a mesma fórmula do retângulo, exceto que a figura tem quatro lados iguais. É assim que você pode encontrar facilmente a dimensão de um lado e um quadrado.
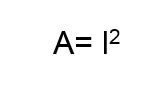
Trapézio
Simplesmente multiplique a altura (h) pelo resultado da soma da maior base com a menor base, representada por B e b, e divida por 2. Ou seja:
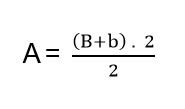
Losango
Multiplique o valor da diagonal principal (D) e a menor (d) e divida o valor por 2.
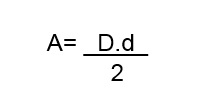
Círculo
O círculo tem a constante p (cerca de 3,14) e o raio (R). Para encontrar sua área, basta aumentar o raio no quadrado e multiplicá-lo pelo valor de p. A fórmula é:
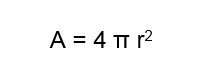
Exercícios de Geometria Plana
1- Temos um triângulo equilátero de lado 6cm. Qual é o perímetro e qual é a área deste triângulo?
Perímetro:
6*3 = 18cm
Área:
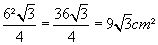
2- Um trapézio tem a base menor igual a 2, a base maior igual a 3 e a altura igual a 10. Qual a área deste trapézio?
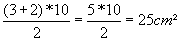
3- Sabendo que a área de um quadrado é 36cm², qual é seu perímetro?
Vamos descobrir o lado do quadrado:
x*x = 36
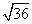
x =
x = 6
Então seu perímetro é 6*4 = 24cm.
4- Calcule a área e o perímetro (em metros) dos retângulos descritos:
a) a = 25 e b = 12
b) a = 14 e b = 10
Resposta a:
Área:
25*12 = 300m²
Perímetro:
25+25+12+12 = 74m
Resposta b:
Área:
14*10 = 140m²
Perímetro:
14+14+10+10 = 48m