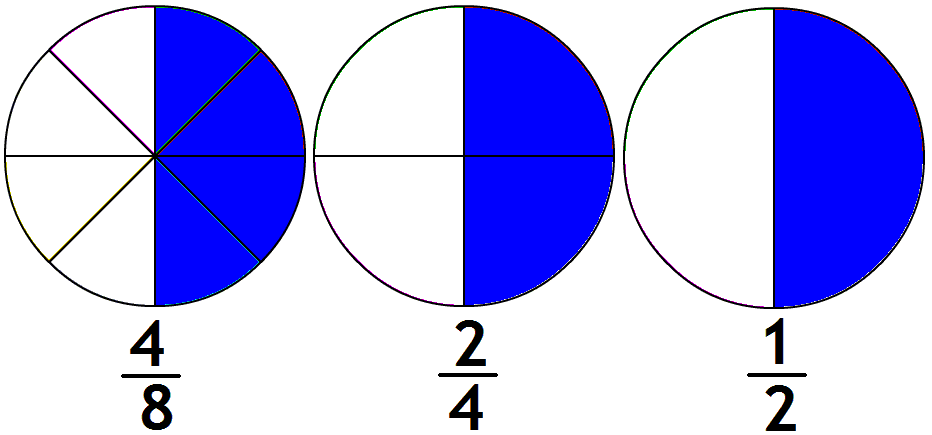
Fração é um modo de expressar uma quantidade a partir de uma razão de dois números inteiros. A palavra fração vem do latim fractus e significa “partido”, dividido ou “quebrado”.
Selecionamos diversos exercícios de frações para que você possa praticar e se aprimorar! Alguns deles caíram em vestibulares.
Exercício 1
Um auxiliar de enfermagem deve trabalhar 30 horas semanais. Devido a um acúmulo de serviço na semana passada, ele precisou fazer 12 horas extras. A fração que corresponde a quanto ele trabalhou a mais do que o previsto é :
a) 1/4.
b) 1/5.
c) 2/5.
d) 2/3.
e) 1/3.
Resposta:
Dados da questão:
Total de horas: 30 horas.
Horas extras: 12 horas
Fração que corresponde à quantidade de horas a mais de trabalho: ? → Esse é o valor que precisa ser encontrado.
Devemos escrever uma fração que represente o que o exercício está solicitando. Essa fração é dada por:
12 : 2=6 : 3 = 2 → A alternativa correta para essa questão é a letra c.
30 : 2 15 : 3 5
Exercícios 2
Uma peça de tecido, após a lavagem, perdeu 1/10 de seu comprimento e ficou medindo 36 metros. Nessas condições, o comprimento, em metros, da peça antes da lavagem era igual a:
a) 39,6 metros
b) 40 metros
c) 41,3 metros
d) 42 metros
e) 42,8 metros
Resposta
Nesse problema precisamos encontrar o valor equivalente a 1/10 do tecido que foi encolhido após a lavagem. Lembre-se que os 36 metros equivalem, portanto, a 9/10.
Se 9/10 é 36, quanto será 1/10?
A partir da regra de três conseguimos obter esse valor:
| 9/10 | 36 metros |
| 1/10 | x |
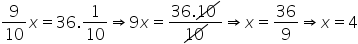
Sabemos então que 1/10 da roupa equivale a 4 metros. Agora, basta somar com os 9/10 restantes:
36 metros (9/10) + 4 metros (1/10) = 40 metros
Resposta: letra b
Exercício 3
Observe a figura:
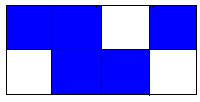
a) Em quantas partes iguais o retângulo foi dividido?
b) Cada uma dessas partes representa que fração do retângulo?
c) A parte pintada representa que fração do retângulo?
Resposta

Exercício 4
A música e a matemática se encontram na representação dos tempos das notas musicais, conforme a figura seguinte.

Um compasso é uma unidade musical composta por determinada quantidade de notas musicais em que a soma das durações coincide com a fração indicada como fórmula do compasso. Por exemplo, se a fórmula de compasso for 1/2, poderia ter um compasso ou com duas semínimas ou uma mínima ou quatro colcheias, poderia ter um compasso ou com duas semínimas ou uma mínima ou quatro colcheias, sendo possível a combinação de diferentes figuras. Um trecho musical de oito compassos, cuja fórmula é 3/4 , poderia ser preenchido com:
a) 24 fusas.
b) 3 semínimas.
c) 8 semínimas.
d) 24 colcheias e 12 semínimas.
e) 16 semínimas e 8 semicolcheias.
Resposta
Para solucionar essa questão, devemos inicialmente calcular quanto vale 8 compassos de 3/4
8 de 3 = 8 x 3 = 24 = 6
4 4 4
Temos então que a alternativa correta para essa questão será aquela que apresentar 6 como resultado da fórmula do compasso.
Por meio do método de tentativas, verificaremos a alternativa correta.
a) 24 fusas
1 fusa = 1 , então 24 fusas de 1 é ?
32 32
24 de 1 = 24 x 1 = 24 : 8 = 3 = 0,75
32 32 32 : 8 4
A alternativa a não é a correta.
b) 3 semínimas
1 semínima = 1 , então 3 semínimas de 1 são?
4 4
3 de 1 = 3 x 1 = 3 = 0,75
4 4 4
A alternativa b não é a correta.
c) 8 semínimas
1 semínima = 1 , então 8 semínimas de 1 são ?
4 4
8 de 1 = 8 x 1 = 8 = 2
4 4 4
A alternativa c não é a correta.
d) 24 colcheias e 12 semínimas.
Na alternativa d, devemos efetuar a soma entre: 24 colcheias + 12 semínimas
1 colcheia = 1 , então 24 colcheias de 1 são ?
8 8
24 de 1 = 24 x 1 = 24 = 3
8 8 8
1 semínima = 1 , então 12 semínimas de 1 são ?
4 4
12 de 1 = 12 x 1 = 12 = 3
4 4 4
24 colcheias + 12 semínimas = 3 + 3 = 6
Obtivemos 6 como resultado da fórmula do compasso. Sendo assim, a alternativa d é a resposta correta para essa questão.
Exercício 5
Tradicionalmente, os paulistas costumam comer pizza nos finais de semana. A família de João, composta por ele, sua esposa e seus filhos, comprou uma pizza tamanho gigante cortada em 20 pedaços iguais. Sabe-se que João comeu 3/12 e sua esposa comeu 2/5 e sobraram N pedaços para seus filhos. O valor de N é?
a) 7
b) 8
c) 9
d) 10
e) 11
Resposta
Sabemos que as frações representam a parte de um todo, que nesse caso são os 20 pedaços de uma pizza gigante.
Para resolver esse problema, temos que obter a quantidade de pedaços correspondente a cada fração:
João: comeu 3/12
Esposa de João: comeu 2/5
N: o que sobrou (?)
Vamos então descobrir quantos pedaços que cada um deles comeu:
João: 3/12 de 20 = 3/12 . 20 = 60/12 = 5 pedaços
Esposa: 2/5 de 20 = 2/5 . 20 = 8 pedaços
Se somarmos os dois valores (5+8 = 13) temos a quantidade de fatias que foram comidas por eles. Portanto, sobraram 7 pedaços que foram divididos entre os filhos.
Resposta: letra a
Exercício 6
Vanessa comprou uma caixa de chocolate e deixou suas amigas, Carla e Mariana, comerem à vontade. Carla comeu 1/7 do total de chocolates. Depois Marina comeu 1/6 do que ficou. Em seguida, Vanessa comeu metade do que havia ficado. Nessa caixa, restam ainda 15 chocolates. Qual é a quantidade total de chocolates que havia na caixa?
Resposta
Para solucionar essa questão, devemos descobrir a quantidade de chocolates que Carla, Marina e Vanessa comeram juntas.
Quantidade de chocolate que Carla comeu: 1 , sobrou 6 .
7 7
Quantidade de chocolate que Mariana comeu: 1 de 6 = 1 . 6 = 6 = 1
6 7 6 7 42 7
Quantidade de chocolate que Vanessa comeu : 5
14
Para saber isso, devemos calcular a quantidade de chocolates que Marina e Carla comeram juntas, que foi:
1 + 1 = 2, sobraram 5 de chocolate na caixa.
7 7 7 7
Desses 5 , Vanessa comeu metade, o que equivale a: 5 : 2 = 5 . 1 = 5
7 7 7 2 14
As três juntas comeram:
1 + 1 + 5 = 2 + 2 + 5 = 9
7 7 14 14 14
Para sabermos o valor inteiro de chocolates que Marina, Carla e Vanessa comeram juntas, basta resolver a regra de três simples abaixo
5 15
14
9 x
14
5 . x = 9 . 15
14 14
5x = 135
x = 135
5
x = 27
Sendo assim, a quantidade total de chocolates dentro da caixa é dada por: 27 + 15 = 42 chocolates.
Exercício 7
Observe as figuras e diga quanto representa cada parte da figura e a parte pintada:
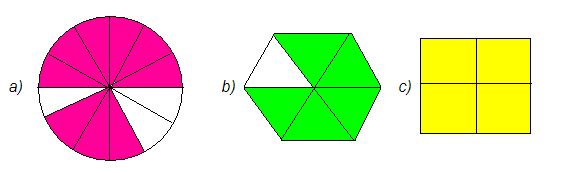
Respostas

Exercício 8
Trinta alunos realizaram uma prova de Química. Deles, 2/5 tiraram a nota acima de oito, 1/3 tirou entre cinco e oito e o restante tirou abaixo de cinco. Calcule a quantidade de alunos que tirou a nota da prova abaixo de cinco.
Resposta
2 de 30 = 2 x 30 = 60 = 12. Doze alunos tiveram a sua nota acima de oito
5 5 5
1 de 30 = 1 x 30 = 30 = 10. Dez alunos tiveram a sua nota entre cinco e oito.
3 3 3
Para saber a quantidade de alunos que tiraram a nota abaixo de cinco, faça:
30 – 12 – 10 = 30 – 22 = 8.
Então 8 alunos tiraram nota abaixo de cinco na avaliação de Química.
Exercício 9
O pantanal é um dos mais valiosos patrimônios naturais do Brasil. É a maior área úmida continental do planeta – com aproximadamente 210 mil km2, sendo 140 mil km2 em território brasileiro, cobrindo parte dos estados de Mato Grosso e Mato Grosso do Sul. As chuvas fortes são comuns nessa região. O equilíbrio desse ecossistema depende, basicamente, do fluxo de entrada e saída de enchentes. As cheias chegam a cobrir até 2/3 da área pantaneira. Durante o período chuvoso, a área alagada pelas enchentes pode chegar a um valor aproximado de:
a) 91,3 mil km2
b) 93,3 mil km2
c) 140 mil km2
d) 152,1 mil km2
e) 233,3 mil km2
Resposta
Primeiramente, devemos anotar os valores oferecidos pelo exercício:
210 mil km2: total da área
2/3 é o valor que as cheias cobrem dessa área
Para resolver basta saber o valor dos 2/3 de 210 mil Km2
210.000 . 2/3 = 420 000/3 = 140 mil km2
Resposta: letra c


