
O empuxo é uma força que exerce um líquido sobre um corpo imerso ou parcialmente submerso. Esta é a força que é responsável, por exemplo, por um pedaço de isopor flutuando na água, e pode ser chamado de flutuabilidade. É também o empuxo que faz um objeto pesado parecer mais leve na água do que realmente é.
O corpo é exposto a duas forças em um fluido: peso e empuxo. Assumindo que é reforçado, é necessário que o empuxo tenha o mesmo módulo, direção e direção em relação ao peso. Portanto, conclui-se que o empuxo é uma força vertical e ascendente.

Seu módulo é dado por:
E=dL⋅vs⋅g
Onde \(d_{L})\ é a densidade do líquido, \(v_{s})\ o volume submerso do corpo, e g é a aceleração da gravidade.
Densidade
A capacidade dos corpos de afundar ou flutuar quando imersos em um líquido (líquido ou gás) depende da densidade (ou massa específica). Densidade é definida como a razão entre massa e volume de um corpo:
d= m
_
v

Sua unidade no sistema internacional é kg/m3, mas também são utilizadas
g/cm3) e\(kg/L). A densidade da água, em temperaturas próximas à ambiente, é
\(1000kg/m3=1kg/L=1g/cm3.
Quando a densidade de um corpo é menor que a do fluido, o corpo flutua. Quando as densidades são as mesmas, o corpo permanece completamente submerso e em equilíbrio. Se a densidade do corpo é maior que a do fluido, o corpo afunda.
| dcorpo < dfluido | Corpo Flutua |
| dcorpo = dfluido | Imerso e em equilíbrio |
| dcorpo > dfluido | Corpo Afunda |
As regras acima também se aplicam à comparação de líquidos! Por exemplo, o óleo flutua na água porque sua densidade é aproximadamente 0,8kg/L0,8kg/L.
Para um corpo estar em equilíbrio nas duas primeiras situações, ele deve ter um peso corporal = flutuabilidade se estas forem as únicas forças atuantes.
Quando a densidade do corpo é muito menor do que a do líquido no qual flutua, uma porção muito pequena do seu volume é submersa. Um exemplo é um balão de natação. Quanto mais a densidade do corpo se aproxima da densidade do fluido, maior a porcentagem do volume submerso.

Princípio de Arquimedes
Arquimedes, um dos principais matemáticos e físicos da Grécia antiga, foi responsável por formular um princípio sobre a flutuabilidade de um corpo. Segundo a lenda, Arquimedes deveria determinar se a coroa obtida pelo rei Heron de Siracusa era feita inteiramente de ouro (como comissionado). Enquanto ele estava na banheira, ele teve a ideia e chamou “Eureka”, que significa “descoberto”.
Sua ideia era colocar a coroa em um recipiente cheio de água e medir o volume transbordado. Então ele mediu o volume, que transbordou com um raio de ouro puro, a mesma massa que a coroa. Quando Arquimedes descobriu que os volumes medidos eram diferentes, descobriu que a coroa estava distorcida porque tinha uma densidade diferente do ouro puro. Como resultado, descobriu-se que a coroa estava parcialmente preenchida com prata pela má intenção do ourives.

Com essa experiência, Arquimedes formulou o princípio de que “todo corpo imerso em um fluido é submetido à ação de uma força vertical e ascendente (empuxo) cuja intensidade corresponde ao peso do fluido deslocado pelo corpo”.
Demonstração da Fórmula
A partir do Princípio de Arquimedes, basta substituir o peso do fluido deslocado por massa ⋅ gravidade e, posteriormente, massa por densidade ⋅ volume chegando a E= dL⋅ vs ⋅ g
Outra abordagem é considerar um corpo prismático submerso e interpretar o empuxo como resultado do diferencial de pressão hidrostática atuando no corpo:
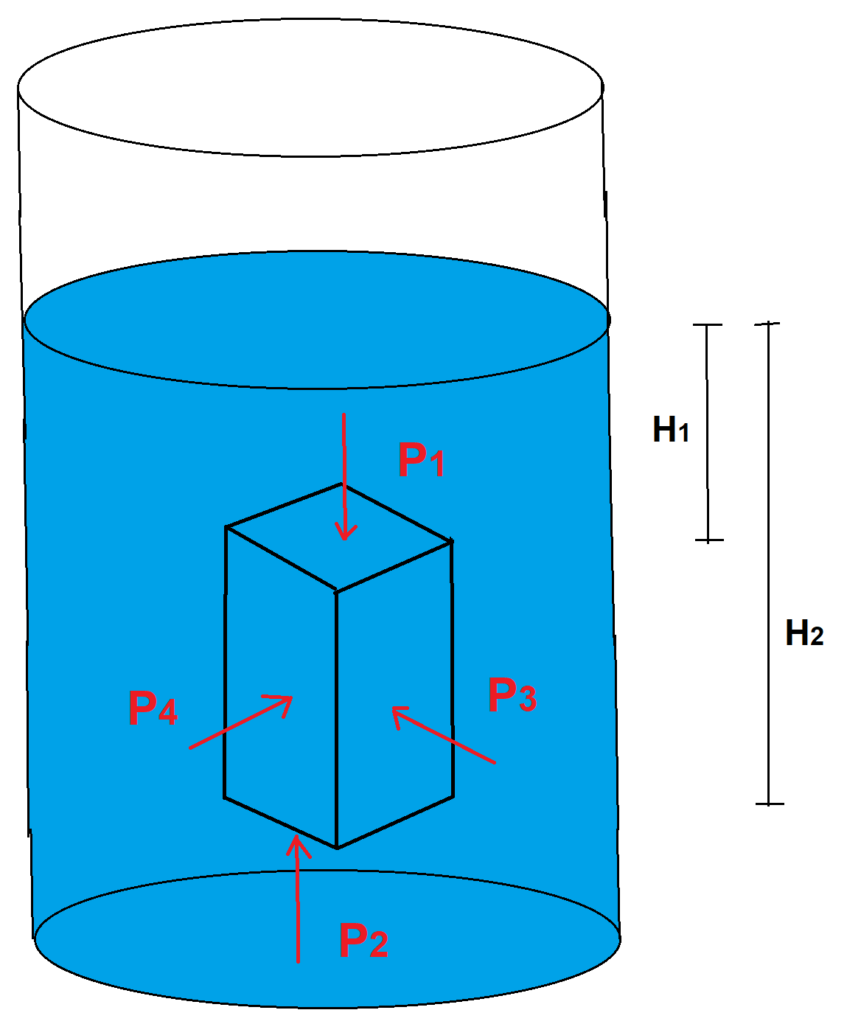
A pressão hidrostática também atua em todas as direções e, portanto, as pressões P3 e P4 são canceladas pelas pressões nas respectivas superfícies opostas.
Já as pressões hidrostáticas P1 e P2 são determinadas pelo princípio de Stevin:
P_{1}=d_{L} \cdot g \cdot H_{1} \hspace{20} P_{2}=d_{L} \cdot g \cdot H_{2}
Como Pressão = Força / Área, e considerando as áreas 1 e 2 iguais:
P_{1} \cdot A = F_{1} =d_{L} \cdot g \cdot A \cdot H_{1} \hspace{20} P_{2} \cdot A = F_{2} =d_{L} \cdot g \cdot A \cdot H_{2}
A força resultante será o empuxo \E = F_{2} – F_{1}\:
E=dL⋅g⋅A⋅(H2−H1)
Como \H_{2} – H{1}\ é igual à altura do corpo, e área vezes a altura é igual ao volume submerso do corpo, chega-se à fórmula:
E=dL⋅vs⋅g
Esta derivada para o módulo de cisalhamento pode ser generalizada para corpos de outras formas, embora em corpos assimétricos o empuxo exerça um momento no centro de gravidade do objeto.
A Queda do Iceberg
Um iceberg flutua porque o gelo (água no estado sólido) tem uma densidade menor que a da água no estado líquido. A densidade da água do mar é de cerca de 1,03 kg / l, enquanto a do gelo é de cerca de 0,92 kg / l. Então, como a diferença entre as densidades não é muito grande, a maior parte do iceberg permanece submersa e cerca de 10% de seu volume é visível acima do nível do mar.

O Gelo Está Nadando
Além do iceberg, um cubo de gelo flutua em um copo de bebida por uma razão muito semelhante ao iceberg, porque sua densidade é menor do que a do líquido.
Analisando a situação do gelo derretendo em um copo de água, descobre-se que o nível de água exibido por alguém observando o vidro não muda. Pode-se imaginar que o gelo desloca um certo volume de água, o que corresponde ao seu peso (princípio de Arquimedes). Como sua massa é retida, o peso do gelo (estado sólido) corresponde ao da água (estado líquido).

No entanto, como o volume deslocado correspondia ao peso, o gelo, quando derretido, consome exatamente o mesmo volume que foi submerso sem aumentar o nível! Como a densidade da água é menor que a do gelo, faz sentido supor que a mesma massa no estado líquido ocupa um volume menor do que no sólido.
Como o Navio Está Flutuando?
Devido ao seu peso considerável, um navio intuitivamente teria uma alta densidade (maior que a da água) e afundaria. Os vasos, no entanto, têm um grande volume submerso e oco. Assim, sua densidade total torna-se menor que a da água (muita massa, mas volume ainda maior) e flutua.
Quanto mais pesado o navio, mais fundo ele tem que navegar, o que é crucial para a construção de portos e canais.


