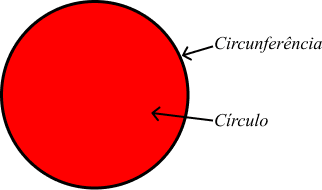
Área é um conceito matemático que pode ser definido como a quantidade de espaço bidimensional, ou seja, superfície.
Existem várias unidades de medida de área, sendo a mais utilizada o metro quadrado (m²) e seus múltiplos e submúltiplos. As medidas agrárias também são amplamente utilizadas: são, o que equivale a cem metros quadrados; e seus múltiplos hectares, o que equivale a dez mil metros quadrados. Outras unidades de medida da área são o acre e o alqueire.
Em geografia e cartografia, o termo “área” corresponde à projeção num plano horizontal de uma parte da superfície terrestre. Assim, a superfície de uma montanha pode ser inclinada, mas sua área é sempre medida em um plano horizontal.

Cada unidade de comprimento tem uma unidade de área correspondente, igual à área do quadrado que tem esse comprimento ao lado. Assim, as áreas podem ser medidas em metros quadrados (²), centímetros quadrados (cm²), milímetros quadrados (mm²), quilômetros quadrados (km²), pés quadrados (ft²), metros quadrados (yd²), milhas quadradas (mi²), etc. Algebricamente, estas unidades são os quadrados das unidades de comprimento correspondentes.
A unidade de superfície do Sistema Internacional é o metro quadrado, que é considerado uma unidade derivada do SI.
Acredita-se que necessidades cotidianas, como a divisão de terras para plantio em margens de rios, a construção de residências, bem como estudos relacionados aos movimentos das estrelas, estejam inseridas no contexto de atividades ligadas à geometria e desenvolvidas pelo homem ao longo da evolução humana.
Entre os principais matemáticos da antiguidade responsáveis pelo desenvolvimento da geometria estão Tales de Milão (VI a.C.), na Grécia, importando a geometria utilizada pelos egípcios; Pitágoras, conhecida pelo teorema aplicado ao retângulo triangular que recebeu seu nome e aperfeiçoou o conceito de demonstração matemática da época. E, já neste século, os “Elementos” de Euclides trouxeram inovações consistentes nos métodos utilizados na antiguidade que contribuíram, há mais de 20 séculos, para o desenvolvimento da ciência, com base em três conceitos básicos, como o ponto, a reta e o círculo, bem como nos cinco postulados. É um sistema axiomático que surge a partir de conceitos e proposições aceitos sem demonstração, conhecidos como postulados e axiomas.

Uma curiosidade interessante dentro do trabalho com áreas refere-se ao corpo humano como uma unidade. Assim, as palmas das mãos, pés, passos, braços e cotovelos foram algumas das primeiras unidades de medida utilizadas direta ou indiretamente. Aproximadamente no ano 3500 B.C., período em que a construção dos primeiros templos na Mesopotâmia e no Egito começou, os responsáveis por esses projetos sentiram a necessidade de encontrar unidades de medida mais regulares e exatas, para então usar como base de medida as partes do corpo de um único homem (por exemplo, o rei) e com essas medidas tornaram-se governantes de madeira e metal, ou mesmo conosco, que se destacou como as primeiras medidas oficiais de comprimento.
O cálculo das superfícies foi possivelmente iniciado pela prática de cobrança de impostos pelos sacerdotes, que intuitivamente calcularam o comprimento dos campos apenas por observação visual, ao longo do tempo observaram os trabalhadores cobrindo uma parte retangular do terreno com pedras quadradas e perceberam que para determinar a quantidade de pedras bastaria contar o número de quadrados em uma linha e multiplicá-lo pelo número de linhas existentes, resultando assim na fórmula para calcular a área de um retângulo, que é obtida do produto da base pela altura.
Pouco depois, desenvolveram uma fórmula para calcular a área de um triângulo, baseada num pensamento muito geométrico, na qual tinham a área de um quadrado ou retângulo e dividindo-a em metades diagonais obtiveram a área do triângulo, de modo que a área do triângulo é dada pela metade da área do quadrado ou retângulo. Quando o terreno não era de forma retangular ou triangular, os primeiros cartógrafos e topógrafos utilizaram a triangulação, que consistia num processo de divisão da área em triângulos, cuja soma das suas áreas representava a área total.

Área do Círculo
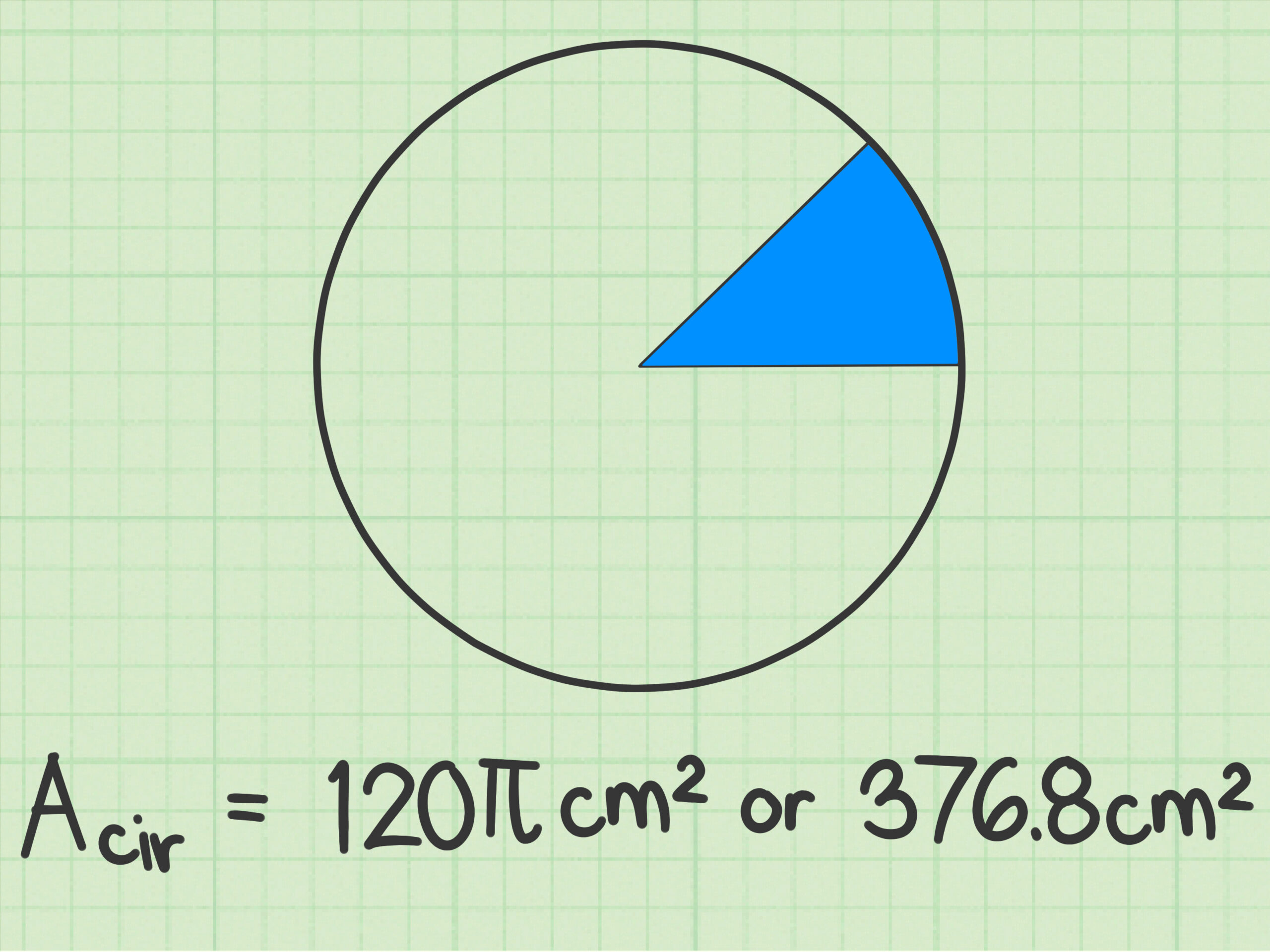
A área do círculo é a medida equivalente à superfície deste valor plano, que é calculada pelo produto entre a medida do raio quadrado (r) e a constante π (3,14).
O círculo, também chamado de disco, em matemática é um conjunto de pontos dentro do círculo. Portanto, a distância entre os pontos da circunferência e o centro é menor ou igual ao tamanho do raio r.
O círculo é formado por meio de um polígono que aumenta seu número de lados. Portanto, quanto mais lados tiver um polígono, mais perto fica de uma forma circular. Veja a imagem abaixo para este processo:
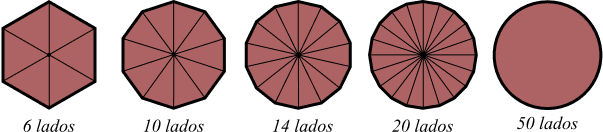
Da imagem podemos ver que o polígono tem vários triângulos e o cálculo da área deste polígono seria igual à soma das áreas de todos os triângulos.
No entanto, quando aumentamos o número de lados, o polígono começa a ter uma forma circular. Portanto, a área deste polígono é equivalente ao cálculo da área de um círculo.
O Que é Circunferência?
A circunferência é composta por um conjunto de pontos que estão distantes do centro C por uma medida r chamada raio. Então a linha que forma a circunferência são pontos com a mesma distância do centro.
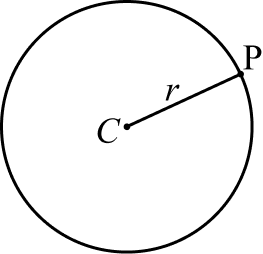
Na imagem vemos que P representa um ponto que está distante do centro C medindo o raio r. Entenda que a reta que forma a circunferência é formada por vários pontos P na mesma distância r do centro C.
A área do círculo é calculada a partir do produto entre a constante π e o raio quadrado (r²). Portanto, temos a seguinte fórmula:
A = π . r²
Onde:
A: é a área;
π: é o número pi (3,14)
r: é a medição do raio.
A área do círculo é igual ao cálculo da área do círculo. Lembre-se que a medida da área do círculo e a área do círculo é uma medida aproximada.
O raio é a medida que vai do centro a um ponto no final da circunferência. Diâmetro é a medida de duas vezes o tamanho do raio, passando pelo centro da circunferência e dividindo-a em duas partes. A medida do diâmetro é 2. π.
Perímetro do Círculo
O perímetro do círculo é o equivalente à linha curva que forma a borda circular. O perímetro é calculado a partir do produto entre o raio e o dobro da constante π. Portanto, temos a seguinte fórmula:
P = 2 . π . r
Onde:
P: É o perímetro;
π: é o número pi (3,14)
É um relâmpago.
O perímetro do círculo é igual ao cálculo do perímetro do círculo. Lembre-se que o perímetro é uma medida aproximada.
Diferença entre Círculo e Circunferência
Há uma sutil diferença entre o círculo e a circunferência. A circunferência trata-se da linha do círculo e o círculo é a parte interna da circunferência.
Como a área do círculo e o círculo são calculados com a mesma fórmula, ele contribui para esta confusão. Mas o círculo é a parte interna e é limitado pelo círculo.