A matemática não é apenas um conjunto de números e fórmulas — ela é uma linguagem que traduz o mundo que nos cerca. Quando observamos uma janela, uma escada, uma rampa ou até mesmo o formato das folhas de uma planta, estamos diante de conceitos geométricos que revelam a harmonia entre forma e função.
Entre os elementos que estruturam essa linguagem, o ângulo ocupa um papel fundamental. Ele é a medida da abertura entre duas retas que se encontram num ponto comum, chamado vértice. Essa simples ideia sustenta o desenho de pontes, o cálculo de terrenos, o design de objetos e até as bases da arte e da arquitetura.
Compreender os ângulos é, portanto, mais do que decorar nomes ou fórmulas: é perceber relações, refletir sobre o espaço e dialogar com o mundo físico e simbólico.
📐 O Que é um Ângulo?
Podemos imaginar um ângulo como o espaço criado entre duas semirretas que partem de um mesmo ponto.
Esse ponto comum é o vértice, e cada uma das semirretas é um lado do ângulo.
💡 Exemplo cotidiano:
Quando abrimos uma porta, o movimento entre a posição fechada e a aberta forma um ângulo. Quanto mais abrimos a porta, maior é o ângulo formado entre ela e a parede.
✏️ Elementos de um Ângulo
| Elemento | Descrição | Exemplo Visual |
|---|---|---|
| Vértice | O ponto de encontro das duas semirretas. | O canto de uma parede. |
| Lados | As semirretas que formam o ângulo. | As bordas da porta aberta e da parede. |
| Abertura Angular | A região entre os lados. | O espaço que a porta cobre ao ser aberta. |
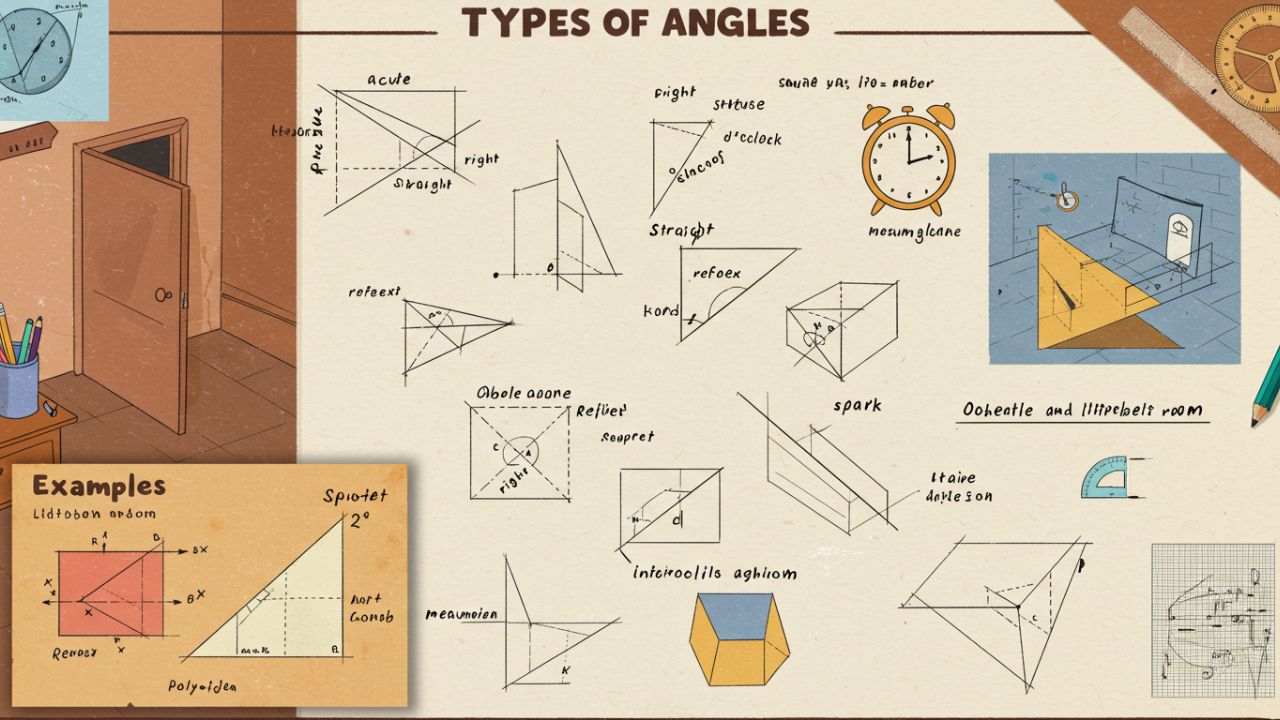
🔍 Como Medimos um Ângulo?
A medida de um ângulo é expressa em graus (°).
Um círculo completo possui 360°, e a partir dessa ideia surgem os principais tipos de ângulos:
| Tipo de Ângulo | Medida em Graus | Descrição | Exemplo do Cotidiano |
|---|---|---|---|
| Nulo | 0° | As semirretas coincidem. | Porta totalmente fechada. |
| Agudo | Menor que 90° | Abertura pequena. | Tesoura quase fechada. |
| Reto | 90° | Forma um “L” perfeito. | Cantos de um livro. |
| Obtuso | Entre 90° e 180° | Abertura maior que a de um ângulo reto. | Porta meio aberta. |
| Raso | 180° | Lados opostos em linha reta. | Porta completamente aberta, alinhada à parede. |
| Côncavo | Entre 180° e 360° | Abertura maior que uma linha reta. | Movimento de uma hélice. |
| Completo | 360° | Abertura total, uma volta completa. | Giro completo de uma roda. |
🧩 Classificação dos Ângulos Segundo Sua Posição
Nem sempre os ângulos aparecem isolados. Em muitas situações, eles se relacionam entre si, e isso muda sua posição e comportamento no plano.
Vejamos as classificações mais importantes:
| Nome | Características | Exemplo |
|---|---|---|
| Adjacentes | Têm o mesmo vértice e um lado em comum, sem se sobrepor. | Cantos de uma janela dupla. |
| Opostos pelo Vértice | Formados por duas retas que se cruzam; possuem medidas iguais. | Cruzamento de ruas. |
| Complementares | A soma das medidas é 90°. | Cantos de uma moldura. |
| Suplementares | A soma das medidas é 180°. | Linha reta dividida por uma semirreta. |
🌈 A Geometria Viva nos Polígonos
Um polígono é uma figura geométrica plana, fechada e formada por segmentos de reta.
Cada ponto onde os lados se encontram forma um ângulo interno, e compreender esses ângulos é essencial para analisar a estrutura das formas.
Exemplos de polígonos e seus ângulos:
| Polígono | Número de Lados | Soma dos Ângulos Internos | Medida de Cada Ângulo (Regular) |
|---|---|---|---|
| Triângulo | 3 | 180° | 60° |
| Quadrilátero | 4 | 360° | 90° |
| Pentágono | 5 | 540° | 108° |
| Hexágono | 6 | 720° | 120° |
| Heptágono | 7 | 900° | ≈128,6° |
| Octógono | 8 | 1080° | 135° |
🧠 Fórmula geral para a soma dos ângulos internos de um polígono: S=(n−2)×180°S = (n – 2) \times 180°S=(n−2)×180°
onde n é o número de lados do polígono.
🎯 Aplicações dos Ângulos na Vida Real
A geometria não é apenas teórica — ela está profundamente enraizada em nossa realidade cotidiana.
Os ângulos são ferramentas de compreensão do espaço, de construção e até de estética.
🏠 1. Arquitetura e Engenharia
Os engenheiros usam ângulos para calcular inclinações, rampas de acessibilidade e resistência de estruturas.
Um pequeno erro angular pode comprometer a segurança de uma ponte ou de um edifício.
🎨 2. Design e Arte
Artistas exploram ângulos para criar perspectiva, simetria e dinamismo visual.
A harmonia das formas depende do diálogo entre ângulos agudos e obtusos.
🧭 3. Navegação e Cartografia
Os navegadores antigos se guiavam pelos ângulos das estrelas e do horizonte.
Ainda hoje, bússolas e instrumentos de medição dependem dessa geometria invisível.
⚙️ 4. Mecânica e Robótica
Engrenagens, braços robóticos e sistemas de movimento usam ângulos para definir trajetórias precisas e sincronizar forças.
📷 5. Fotografia e Cinema
A escolha do ângulo de uma câmera muda totalmente a narrativa visual.
Um ângulo alto transmite vulnerabilidade; um ângulo baixo, poder e imponência.
🔢 Exercício Reflexivo
Imagine que você está desenhando um triângulo equilátero e, em seguida, um quadrado.
Agora, feche os olhos e tente perceber como o espaço muda de um para o outro.
O triângulo parece apontar, buscar o alto — o quadrado, em contrapartida, é estável, firme.
💭 Reflexão:
O estudo dos ângulos não serve apenas para resolver problemas matemáticos, mas para compreender formas de equilíbrio, direção e movimento — na natureza, na arte e até em nossa própria vida.
🧮 Exercícios de Fixação
1️⃣ Calcule a soma dos ângulos internos de:
a) Um decágono
b) Um heptágono
c) Um dodecágono S=(n−2)×180°S = (n – 2) \times 180°S=(n−2)×180°
2️⃣ Determine o tipo de ângulo em cada situação:
a) O relógio marca 3h → ____
b) Um cruzamento em “T” → ____
c) Uma rampa suave → ____
3️⃣ Relacione:
| Situação | Tipo de Ângulo |
|---|---|
| Rampa de acesso | Obtuso |
| Quadro de parede | Reto |
| Garfo aberto | Agudo |
🌍 A Geometria como Prática Libertadora
A educação não pode limitar-se à transmissão de fórmulas prontas.
O verdadeiro aprendizado nasce do diálogo entre o aluno e o mundo que ele habita.
Quando o estudante entende que os ângulos estão na casa onde vive, nas ruas que percorre e até nas obras que admira, a matemática deixa de ser abstrata — ela se torna viva.
A compreensão dos ângulos é um convite à leitura do espaço, à descoberta da beleza das formas e à construção do pensamento crítico.
📚 Aprender ângulos é aprender a ver.
Ver com mais clareza.
Ver com mais consciência.
Ver com mais liberdade.
🧭 Conclusão
Os ângulos são os elos invisíveis que unem a arte, a ciência e o cotidiano.
Estudá-los é perceber que cada abertura, cada curva e cada encontro de linhas guarda uma intenção, uma harmonia, uma lógica.
Quando a geometria se torna diálogo, o aluno deixa de ser um espectador e passa a ser autor do próprio conhecimento.
E assim, entre vértices e lados, descobre-se não apenas o valor de um ângulo, mas o sentido do aprender.