
A cinemática é o ramo da mecânica clássica que descreve o movimento de pontos, objetos e sistemas de grupos de objetos, sem referência às causas do movimento (isto é, forças). O estudo da cinemática é muitas vezes referido como a “geometria do movimento”.
Objetos estão em movimento ao nosso redor. Tudo, desde uma partida de tênis até um sobrevoo espacial ao planeta Marte, envolve movimento. Quando você está descansando, seu coração move o sangue em suas veias. Mesmo em objetos inanimados, há movimento contínuo nas vibrações de átomos e moléculas. Perguntas interessantes sobre o movimento podem surgir: quanto tempo levará para uma sonda espacial para viajar para Marte? Onde uma bola de futebol se lançará em um certo ângulo? Uma compreensão do movimento, no entanto, também é fundamental para entender outros conceitos da física. Uma compreensão da aceleração, por exemplo, é crucial para o estudo da força.

Para descrever o movimento, a cinemática estuda as trajetórias de pontos, linhas e outros objetos geométricos, bem como suas propriedades diferenciais (como velocidade e aceleração). A cinemática é usada na astrofísica para descrever o movimento de corpos e sistemas celestes; e em engenharia mecânica, robótica e biomecânica para descrever o movimento de sistemas compostos de partes unidas (como um motor, um braço robótico ou o esqueleto do corpo humano).
Um estudo formal da física começa com a cinemática. A palavra “cinemática” vem de uma palavra grega “kinesis”, que significa movimento, e está relacionada a outras palavras em inglês, como “cinema” (filmes) e “cinesiologia” (o estudo do movimento humano). A análise cinemática é o processo de medir as quantidades cinemáticas usadas para descrever o movimento. O estudo da cinemática pode ser resumido em expressões puramente matemáticas, que podem ser usadas para calcular vários aspectos do movimento, como velocidade, aceleração, deslocamento, tempo e trajetória.
Escolher um quadro de referência requer decidir onde a posição inicial do objeto é e qual direção será considerada positiva. Os quadros de referência válidos podem diferir um do outro movendo-se um em relação ao outro. Quadros de referência são particularmente importantes quando se descreve o deslocamento de um objeto.

Deslocamento é a mudança na posição de um objeto em relação ao seu quadro de referência. Quadro de referência é um sistema de coordenadas ou conjunto de eixos dentro do qual medir a posição, orientação e outras propriedades de objetos nele.
Para descrever o movimento de um objeto, você deve primeiro descrever sua posição – onde está em qualquer momento particular. Mais precisamente, você precisa especificar sua posição em relação a um quadro de referência conveniente. A Terra é frequentemente usada como referencial, e freqüentemente descrevemos a posição de objetos relacionados à sua posição de e para a Terra. Matematicamente, a posição de um objeto é geralmente representada pela variável x .

Quadros de Referência
Existem duas escolhas que você deve fazer para definir uma variável de posição x . Você tem que decidir onde colocar x = 0 e qual direção será positiva. Isso é chamado de escolher um sistema de coordenadas ou escolher um quadro de referência. Contanto que você seja consistente, qualquer quadro é igualmente válido. Mas você não quer mudar os sistemas de coordenadas no meio de um cálculo.
Imagine-se sentado em um trem em uma estação quando de repente você percebe que a estação está se movendo para trás. A maioria das pessoas diria que eles simplesmente não perceberam que o trem estava em movimento – parecia apenas que a estação estava se movendo. Mas isso mostra que há uma terceira escolha arbitrária que entra na escolha de um sistema de coordenadas: quadros de referência válidos podem diferir um do outro movendo-se um em relação ao outro. Pode parecer estranho usar um sistema de coordenadas se movendo em relação à Terra – mas, por exemplo, a estrutura de referência que se move junto com um trem pode ser muito mais conveniente para descrever as coisas que acontecem dentro do trem. Quadros de referência são particularmente importantes quando se descreve o deslocamento de um objeto.

Deslocamento é a mudança na posição de um objeto em relação ao seu quadro de referência. Por exemplo, se um carro se desloca de uma casa para uma mercearia, seu deslocamento é a distância relativa da mercearia ao quadro de referência ou à casa. A palavra “deslocamento” implica que um objeto se moveu ou foi deslocado. Deslocamento é a mudança na posição de um objeto e pode ser representado matematicamente da seguinte maneira:
Δ x = x f – x 0Δx=xf-x0
Onde Δ x é o deslocamento, x f é a posição final e x 0 é a posição inicial. Isso mostra a importância de usar um quadro de referência ao descrever o deslocamento de um passageiro em um avião.
Qual é a diferença entre distância e deslocamento? Enquanto o deslocamento é definido pela direção e magnitude, a distância é definida apenas pela magnitude. Deslocamento é um exemplo de uma quantidade vetorial. Distância é um exemplo de uma grandeza escalar. Um vetor é qualquer quantidade com magnitude e direção. Outros exemplos de vetores incluem uma velocidade de 90 km / h a leste e uma força de 500 newtons diretamente abaixo.

Há uma variedade de quantidades associadas ao movimento de objetos – deslocamento (e distância), velocidade, aceleração e tempo. O conhecimento de cada uma dessas quantidades fornece informações descritivas sobre o movimento de um objeto. Por exemplo, se um carro é conhecido por se mover com uma velocidade constante de 22,0 m / s, Norte por 12,0 segundos para um deslocamento para o norte de 264 metros, então o movimento do carro é totalmente descrito. E se um segundo carro é conhecido por acelerar a partir de uma posição de descanso com uma aceleração para o leste de 3,0 m / s 2por um tempo de 8,0 segundos, proporcionando uma velocidade final de 24 m / s, leste e um deslocamento para o leste de 96 metros, então o movimento deste carro é totalmente descrito.
Essas duas instruções fornecem uma descrição completa do movimento de um objeto. No entanto, tal completude nem sempre é conhecida. Muitas vezes, é o caso de apenas alguns parâmetros do movimento de um objeto serem conhecidos, enquanto o restante é desconhecido. Por exemplo, quando você se aproxima do semáforo, você pode saber que seu carro tem uma velocidade de 22 m / s, leste e é capaz de uma aceleração de derrapagem de 8,0 m / s 2Oeste No entanto, você não conhece o deslocamento que seu carro experimentaria se batesse com os freios e parasse; e você não sabe o tempo necessário para derrapar até parar. Em um exemplo como esse, os parâmetros desconhecidos podem ser determinados usando princípios físicos e equações matemáticas (as equações cinemáticas).

As Fórmulas de Cinemática
As equações cinemáticas, ou fórmulas de cinemática, são um conjunto de quatro equações que podem ser utilizadas para prever informações desconhecidas sobre o movimento de um objeto, se outras informações forem conhecidas. As equações podem ser utilizadas para qualquer movimento que possa ser descrito como sendo um movimento de velocidade constante (uma aceleração de 0 m / s / s) ou um movimento de aceleração constante. Eles nunca podem ser usados durante qualquer período de tempo durante o qual a aceleração está mudando. Cada uma das equações cinemáticas inclui quatro variáveis.
Se os valores de três das quatro variáveis forem conhecidos, então o valor da quarta variável pode ser calculado. Dessa maneira, as equações cinemáticas fornecem um meio útil de prever informações sobre o movimento de um objeto, se outras informações forem conhecidas. Por exemplo, se o valor de aceleração e os valores iniciais e finais de velocidade de um carro derrapante forem conhecidos, então o deslocamento do carro e o tempo podem ser previstos usando as equações cinemáticas. A lição 6 desta unidade enfocará o uso das equações cinemáticas para prever os valores numéricos de quantidades desconhecidas para o movimento de um objeto.
As quatro equações cinemáticas que descrevem o movimento de um objeto são:
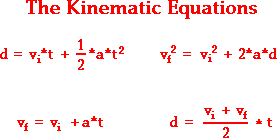
Há uma variedade de símbolos usados nas equações acima. Cada símbolo tem seu próprio significado específico. O símbolo d representa o deslocamento do objeto. O símbolo t representa o tempo para o qual o objeto foi movido. O símbolo a representa a aceleração do objeto. O símbolo v representa a velocidade do objeto; um subscrito de i depois de v (como em v i ) indica que o valor de velocidade é o valor de velocidade inicial e um subscrito de f (como em v f ) indica que o valor de velocidade é o valor de velocidade final.
Cada uma dessas quatro equações descreve adequadamente a relação matemática entre os parâmetros do movimento de um objeto. Como tal, eles podem ser usados para prever informações desconhecidas sobre o movimento de um objeto se outras informações forem conhecidas.



