
Uma progressão aritmética é uma sequência de números em que os termos consecutivos (começando com o segundo termo) são formados pela adição de uma quantidade constante com o termo precedente.
Uma sequência de números é conhecida como uma progressão aritmética (AP) se a diferença do termo e o termo precedente forem sempre iguais ou constantes.
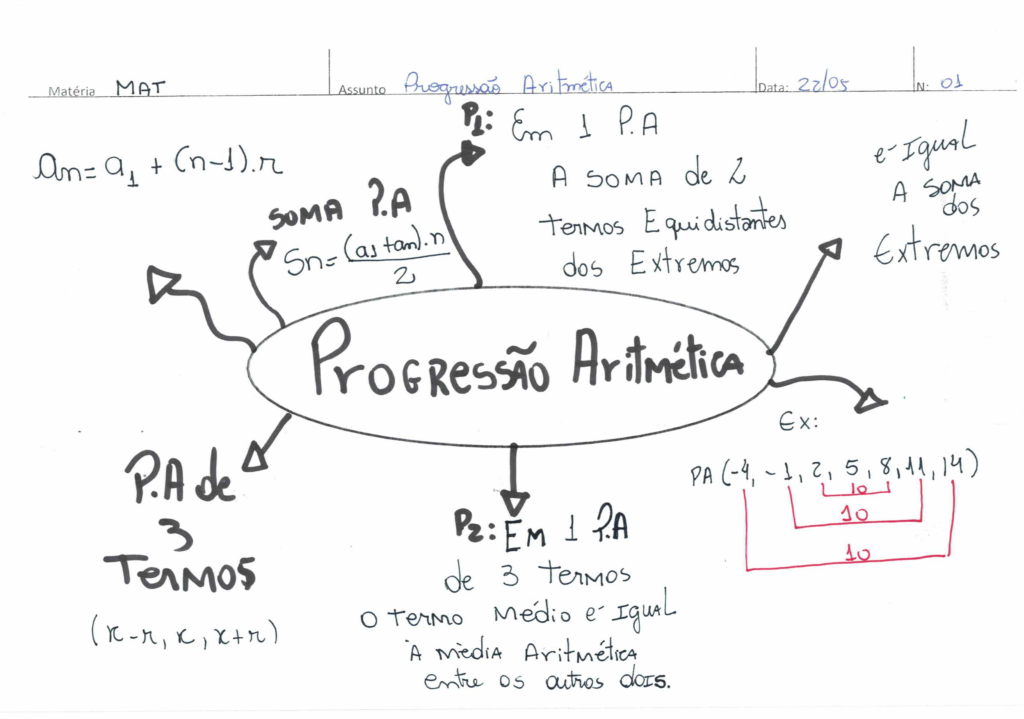
A quantidade constante indicada na definição acima é chamada de diferença comum da progressão. A diferença constante, geralmente denotada por d, é chamada de diferença comum.
uman + 1n+1 – umann = constante (= d) para todos n∈ N
A partir da definição, é claro que uma progressão aritmética é uma sequência de números em que a diferença entre quaisquer dois termos consecutivos é constante.
A progressão aritmética é usada em toda a matemática e aplicada a problemas de engenharia, ciências, ciências da computação, biologia e finanças. Um conjunto de problemas e exercícios envolvendo sequências aritméticas, juntamente com soluções detalhadas e respostas, são apresentados.

Exemplos de progressão aritmética:
1. -2, 1, 4, 7, 10 ……………. é um AP cujo primeiro termo é -2 e a diferença comum é 1 – (-2) = 1 + 2 = 3.
2. A sequência {3, 7, 11, 15, 19, 23, 27, …………………} é uma progressão aritmética cuja diferença comum é 4, uma vez que
Segundo termo (7) = primeiro termo (3) + 4
Termo Terceiro (11) = Segundo Termo (7) + 4
Quarto termo (15) = terceiro termo (11) + 4
Quinto termo (19) = quarto termo (15) + 4 etc.
3. A sequência {58, 43, 28, 13, -2, -17, -32, …………………} é uma progressão aritmética cuja diferença comum é -15, uma vez que
Segundo termo (43) = Primeiro termo (58) + (-15)
Terceiro termo (28) = segundo termo (43) + (-15)
Quarto termo (13) = terceiro termo (28) + (-15)
Quinto termo (-2) = quarto termo (13) + (-15) etc.
4. A sequência {11, 23, 35, 47, 59, 71, 83, …………………} é uma progressão aritmética cuja diferença comum é 4, uma vez que
Segundo termo (23) = primeiro termo (11) + 12
Terceiro termo (35) = segundo termo (23) + 12
Quarto mandato (47) = terceiro mandato (35) + 12
Quinto termo (59) = quarto termo (47) + 12 etc.
Algoritmo para determinar se uma sequência é uma progressão aritmética ou não quando o seu enésimo termo é dado:
Etapa I: obter umnn
Etapa II: Substitua n por n + 1 em umnn para obter umn + 1n+1.
Etapa III: calcular umn + 1n+1 – umann.
Quando umn + 1n+1 é independente de n então, a sequência dada é uma progressão aritmética. E quando umn + 1n+1 não é independente de n então, a sequência dada não é uma progressão aritmética.

Os exemplos a seguir ilustram o conceito acima:
1. Mostre que a sequência <ann> definido por umnn= 2n + 3 é uma progressão aritmética. Também bem a diferença comum.
Solução:
A sequência dada ann = 2n + 3
Substituindo n por (n + 1), obtemos
uman + 1n+1 = 2 (n + 1) + 3
uman + 1n+1 = 2n + 2 + 3
uman + 1n+1 = 2n + 5
Agora, umn + 1n+1 – umann = (2n + 5) – (2n + 3) = 2n + 5 – 2n – 3 = 2
Portanto, umn + 1n+1 – umanné independente de n, que é igual a 2.
Portanto, a sequência dada ann = 2n + 3 é uma progressão aritmética com diferença comum 2.
2. Mostre que a sequência <ann> definido por umnn = 3n22 + 2 não é uma progressão aritmética.
Solução:
A sequência dada ann = 3n22 + 2
Substituindo n por (n + 1), obtemos
uman + 1n+1 = 3 (n + 1)22 + 2
uman + 1n+1 = 3 (n22 + 2n + 1) + 2
uman + 1n+1 = 3n22 + 6n + 3 + 2
uman + 1n+1 = 3n22 + 6n + 5
Agora, umn + 1n+1 – umann = (3n22 + 6n + 5) – (3n22 + 2) = 3n22 + 6n + 5 – 3n22 – 2 = 6n + 3
Portanto, umn + 1n+1 – umann não é independente de n.
Daí umn + 1n+1 – umann não é constante.
Assim, a sequência dada ann = 3n22 + 2 não é uma progressão aritmética.
Nota: Para obter a diferença comum de uma determinada progressão aritmética, é necessário subtrair qualquer termo daquele que o segue. Isso é,
Diferença Comum = Qualquer termo – Seu termo anterior.

Exercícios Sobre Progressão Aritmética
Exercício 1 – O primeiro termo de uma sequência aritmética é igual a 6 e a diferença comum é igual a 3. Encontre uma fórmula para o enésimo termo e o valor do 50º termo.
Solução para o Problema 1: Use o valor da diferença comum d = 3 e o primeiro termo a 1 = 6 na fórmula para o enésimo termo dado acima
a_n = a_1 + (n – 1) d \\ = 6 + 3 (n – 1) \\ = 3 n + 3
O 50º termo é encontrado definindo n = 50 na fórmula acima.
a_ {50} = 3 (50) + 3 = 153
Exercício 2 – O primeiro termo de uma sequência aritmética é igual a 200 e a diferença comum é igual a -10. Encontre o valor do 20º termo.
Solução para o Problema 2: Use o valor da diferença comum d = -10 e o primeiro termo a 1= 200 na fórmula para o n-ésimo termo dado acima e então aplique-o no 20º termo
a 20 = 200 + (-10) (20 – 1) = 10
Exercício 3 – Uma sequência aritmética tem uma diferença comum igual a 10 e seu 6º termo é igual a 52. Encontre seu 15º termo.
Solução para o Problema 3: Usamos a fórmula do enésimo termo para o 6º termo, que é conhecido, para escrever
um 6 = 52 = a 1 + 10 (6 – 1)
A equação acima nos permite calcular um 1 .
a 1 = 2
Agora que conhecemos o primeiro termo e a diferença comum, usamos a fórmula do n-ésimo termo para encontrar o 15º termo como segue.
a 15 = 2 + 10 (15 – 1) = 142
Exercício 4 – Uma sequência aritmética tem seu 5º termo igual a 22 e seu 15º termo igual a 62. Encontre seu 100º termo.
Solução para o Problema 4: Usamos a fórmula do nésimo prazo para o 5º e 15º termos para escrever
um 5 = a 1 + (5 – 1) d = 22
a 15 = a 1 + (15 – 1) d = 62
Obtemos um sistema de 2 equações lineares onde o desconhecido é 1 e d. Subtraia o termo direito e esquerdo das duas equações para obter
62 – 22 = 14 d – 4 d
resolva para d.
d = 4
Agora use o valor de d em uma das equações para encontrar um 1 .
a 1 + (5 – 1) 4 = 22
Resolva para 1 para obter
a 1 = 6
Agora que calculamos um 1 ed usamos na fórmula do n-ésimo termo para encontrar a 100ª fórmula.
a 100 = 6 + 4 (100 – 1) = 402
Exercício 5 – Encontre a soma de todos os inteiros de 1 a 1000.
Solução para o Problema 5: A sequência de inteiros começando de 1 a 1000 é dada por
1, 2, 3, 4, …, 1000
A sequência acima tem 1000 termos. O primeiro termo é 1 e o último termo é 1000 e a diferença comum é igual a 1. Temos a fórmula que dá a soma dos primeiros n termos de uma sequência aritmética, conhecendo o primeiro e o último termo da sequência e o número de termos (veja a fórmula acima).
s 1000 = 1000 (1 + 1000) / 2 = 500500
Exercício 6 – Encontre a soma dos primeiros 50 inteiros positivos iguais.
Solução para o Problema 6: A sequência dos primeiros 50 inteiros positivos iguais é dada por
2, 4, 6, …
A sequência acima tem um primeiro termo igual a 2 e uma diferença comum d = 2. Usamos a fórmula do termo n para encontrar o 50º termo
a 50 = 2 + 2 (50 – 1) = 100
Agora, o primeiro termo e último termo e o número de termos na sequência, agora encontramos a soma dos primeiros 50 termos
s 50 = 50 (2 + 100) / 2 = 2550
Exercício 7 – Encontre a soma de todos os inteiros positivos, de 5 a 1555 inclusive, que são divisíveis por 5.
Solução para o Problema 7: Os primeiros poucos termos de uma seqüência de inteiros positivos divisíveis por 5 são dados por
5, 10, 15,. ..
A sequência acima tem um primeiro termo igual a 5 e uma diferença comum d = 5. Precisamos saber a classificação do termo 1555. Usamos a fórmula para o enésimo termo como segue
1555 = a 1 + (n – 1) d
Substitua a 1 ed por seus valores
1555 = 5 + 5 (n – 1)
Resolva para n para obter
n = 311
Agora sabemos que 1555 é o 311º termo, podemos usar a fórmula para a soma da seguinte forma
s 311 = 311 (5 + 1555) / 2 = 242580
Exercício 8 – Encontre a soma S definida porS = \ sum_ {n = 1} ^ {10} (2n + 1/2)
Solução para o Problema 8: Vamos primeiro decompor esta soma da seguinte forma
S = \ sum_ {n = 1} ^ {10} (2n + 1/2)
= 2 \ sum_ {n = 1} ^ {10} n + \ sum_ {n = 1} ^ {10} (1/2)
O termo n é a soma dos primeiros 10 inteiros positivos. Os 10 primeiros números inteiros positivos fazem uma sequência arirmética com primeiro termo igual a 1, tem n = 10 termos e seu 10º termo é igual a 10. Esta soma é obtida usando a fórmula s n = n (a 1 + a n ) / 2 como segue
10 (1 + 10) / 2 = 55
O termo ∑ (1/2) é a adição de um termo constante 10 vezes e é dado por
10 (1/2) = 5
A soma S é dada por
S = 2 (55) + 5 = 115


