Exercícios Sobre Função Do 2° Grau [Matemática]

Na matemática, uma função quadrática, um polinômio quadrático, um polinômio de 2º grau ou simplesmente um quadrático, é uma função polinomial com uma ou mais variáveis em que o termo de maior grau é do segundo grau. Por exemplo, uma função quadrática em três variáveis X , Y, e Z contém exclusivamente termos x ², y ², Z ², xy, xz, yz, x, y, ze uma constante:

f (x, y, z) = ax ^ {2} + por ^ {2} + cz ^ {2} + dxy + exz + fyz + gx + hy + iz + j,

Com pelo menos um dos coeficientes a, b, c, d, e ou f dos termos de segundo grau sendo diferentes de zero.

Uma função quadrática univariada (variável simples) tem a forma

f (x) = ax ^ {2} + bx + c, \ quad a \ neq 0

na variável única x. O gráfico de uma função quadrática univariada é uma parábola cujo eixo de simetria é paralelo ao eixo y , como mostrado à direita.

Se a função quadrática for igual a zero, o resultado será uma equação quadrática. As soluções para a equação univariada são chamadas de raízes da função univariada.

O caso bivariado em termos de variáveis x e y tem a forma

f (x, y) = ax ^ {2} + por ^ {2} + cxy + dx + ey + f \, \!

com pelo menos um de a, b, c não é igual a zero, e uma equação definindo essa função como zero dá origem a uma seção cônica (um círculo ou outra elipse, uma parábola ou uma hipérbole).

Em geral, pode haver um número arbitrariamente grande de variáveis, em cujo caso a superfície resultante é chamada de quadrática, mas o grau mais alto deve ser de grau 2, como x ², xy, yz, etc.

O adjetivo quadrático vem da palavra latina quadrātum (quadrado). Um termo como x ² é chamado de quadrado na álgebra porque é a área de um quadrado com o lado x .

Coeficientes

Os coeficientes de um polinômio são freqüentemente considerados números reais ou complexos, mas na verdade, um polinômio pode ser definido sobre qualquer anel.

Grau

Ao usar o termo “polinômio quadrático”, os autores às vezes significam “ter grau exatamente 2”, e às vezes “ter grau no máximo 2”. Se o grau for menor que 2, isso pode ser chamado de “caso degenerado”. Normalmente, o contexto estabelecerá qual dos dois se destina.

Às vezes, a palavra “ordem” é usada com o significado de “grau”, por exemplo, um polinômio de segunda ordem.

Variáveis

Um polinomial quadrática pode envolver uma única variável x (o caso univariada), ou várias variáveis, tais como x , y , e z (caso multivariada).

O caso de uma variável

Qualquer polinômio quadrático de variável única pode ser escrito como

onde x é a variável e a, b e c representam os coeficientes. Na álgebra elementar, tais polinômios frequentemente surgem na forma de uma equação quadrática ax² + bx + c = 0. As soluções para essa equação são chamadas de raízes do polinômio quadrático, e podem ser encontradas através da fatoração , completando o quadrado, o gráfico, o método de Newton , ou através do uso da fórmula quadrática . Cada polinômio quadrático tem uma função quadrática associada, cujo gráfico é uma parábola.

Caso bivariado

Qualquer polinômio quadrático com duas variáveis pode ser escrito como

onde x e y são as variáveis e a , b , c , d , e e f são os coeficientes. Tais polinômios são fundamentais para o estudo das seções cônicas, que se caracterizam por equacionar a expressão de f ( x , y ) a zero. Similarmente, polinômios quadráticos com três ou mais variáveis correspondem a superfícies quadráticas e hipersuperfícies. Na álgebra linear, os polinômios quadráticos podem ser generalizados para a noção de uma forma quadrática em um espaço vetorial.

Formas de uma função quadrática univariada

Uma função quadrática univariada pode ser expressa em três formatos:

f (x) = ax² + bx + c é chamado de formulário padrão
f (x) = a (x – r ₁) (x – r ₂) é chamado de forma fatorada, onde r ₁ e r ₂ são as raízes da função quadrática e as soluções da equação quadrática correspondente.
f (x) = a (x – h)² + k chama-se a forma de vértice, em que h e k são as x e y coordenadas do vértice, respectivamente.

O coeficiente a é o mesmo valor nas três formas. Para converter a forma padrão para forma consignado, um precisa apenas a fórmula quadrática para determinar as duas raízes de r ₁ e r ₂ . Para converter o formulário padrão em formulário de vértice, é necessário um processo chamado completando o quadrado. Para converter a forma fatorada (ou formulário de vértice) em formulário padrão, é necessário multiplicar, expandir e / ou distribuir os fatores.

Gráfico da função univariada

Independentemente do formato, o gráfico de uma função quadrática univariada {\ displaystyle f (x) = ax ^ {2} + bx + c}é uma parábola (como mostrado à direita). Equivalentemente, este é o gráfico da equação quadrática bivariada y = ax ^ {2} + bx + c.

Se a > 0 , a parábola se abre para cima.
Se um <0 , a parábola se abre para baixo.

O coeficiente a controla o grau de curvatura do gráfico; uma magnitude maior de a dá ao gráfico uma aparência mais fechada (nitidamente curva).

Os coeficientes b e a controlam juntos a localização do eixo de simetria da parábola (também a x- coordenada do vértice) que está em

$x = - {\ frac {b} {2a}}.$

O coeficiente c controla a altura da parábola; mais especificamente, é a altura da parábola onde ela intercepta o eixo y .

Vértice

O vértice de uma parábola é o lugar onde ela gira; Por isso, também é chamado de ponto de virada . Se a função quadrática estiver na forma de vértice, o vértice será ( h , k ) . Usando o método de completar o quadrado, pode-se transformar o formulário padrão

para dentro

{\ displaystyle {\ begin {alinhados} f (x) e = ax ^ {2} + bx + c \\ & = a (xh) ^ {2} + k \\ & = a \ left (x - {\ frac {-b} {2a}} \ right) ^ {2} + \ left (c - {\ frac {b ^ {2}} {4a}} \ right), \\\ end {alinhado}}}

então o vértice (h, k) da parábola na forma padrão é

{\ displaystyle \ left (- {\ frac {b} {2a}}, c - {\ frac {b ^ {2}} {4a}} \ right).}

Se a função quadrática estiver na forma fatorada

a média das duas raízes, ie

é a x- coordenada do vértice e, portanto, o vértice ( h , k ) é

\ left ({\ frac {r_ {1} + r_ {2}} {2}}, f \ left ({\ frac {r_ {1} + r_ {2}} {2}} \ right) \ right) . \!

O vértice também é o ponto máximo se um <0 , ou o ponto mínimo se a > 0 .

A linha vertical

que passa pelo vértice é também o eixo de simetria da parábola.

Pontos máximos e mínimos

Usando o cálculo, o ponto do vértice, sendo um máximo ou mínimo da função, pode ser obtido encontrando as raízes da derivada

{\ displaystyle f (x) = ax ^ {2} + bx + c \ quad \ Rightarrow \ quad f '(x) = 2ax + b \, \ !.}

x é uma raiz de f ‘( x ) se f ‘ ( x ) = 0 resultando em

com o valor da função correspondente

{\ displaystyle f (x) = a \ left (- {\ frac {b} {2a}} \ right) ^ {2} + b \ left (- {\ frac {b} {2a}} \ right) + c = c - {\ frac {b ^ {2}} {4a}} \, \ !,}

mais uma vez as coordenadas do ponto de vértice, ( h , k ) , podem ser expressas como

A raiz quadrada de uma função quadrática univariada

A raiz quadrada de uma função quadrática univariada dá origem a uma das quatro seções cônicas, quase sempre a uma elipse ou a uma hipérbole.

E se a > 0 então a equação

$y = \ pm {\ sqrt {ax ^ {2} + bx + c}}$

descreve uma hipérbole, como pode ser visto pela quadratura de ambos os lados. As direções dos eixos da hipérbole são determinadas pela ordenada do ponto mínimo da parábola correspondente

$y_ {p} = ax ^ {2} + bx + c \, \!$

Se a ordenada é negativa, então o eixo maior da hipérbole (através de seus vértices) é horizontal, enquanto se a ordenada é positiva, o eixo maior da hipérbole é vertical.

E se a < 0 então a equação

$y = \ pm {\ sqrt {ax ^ {2} + bx + c}}$

descreve um círculo ou outra elipse ou nada. Se a ordenada do ponto máximo da parábola correspondente

é positivo, então sua raiz quadrada descreve uma elipse, mas se a ordenada é negativa, então ela descreve um lugar vazio de pontos.

Exercícios Sobre Função Do 2° Grau

As raízes da equação 2x²+ bx + c = 0 são 3 e − 4. Nesse caso, o valor de b – c é:

a) −26.
b) −22.
c) −1.
d) 22.
e) 26.

As raízes de uma equação do 2º grau correspondem aos valores de x em que o resultado da equação é igual a zero.

Portanto, substituindo o x pelos valores das raízes poderemos encontrar o valor de b e c. Fazendo isso, ficaremos com o seguinte sistema de equações:

Subtraindo os valores encontrados, temos:

b – c = 2 – (-24) = 26

Alternativa e) 26

2) A igreja de São Francisco de Assis, obra arquitetônica modernista de Oscar Niemeyer, localizada na Lagoa da Pampulha, em Belo Horizonte, possui abóbadas parabólicas. A seta na Figura 1 ilustra uma das abóbadas na entrada principal da capela. A figura 2 fornece uma vista frontal desta abóbada, com medidas hipotéticas para simplificar os cálculos.

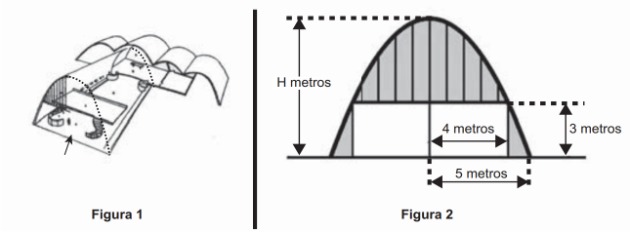
Qual a medida da altura H, em metro, indicada na Figura 2?

a) 16/3
b) 31/5
c) 25/4
d) 25/3
e) 75/2

Nesta questão precisamos calcular o valor da altura. Para isso, vamos representar a parábola no eixo cartesiano, conforme figura abaixo.

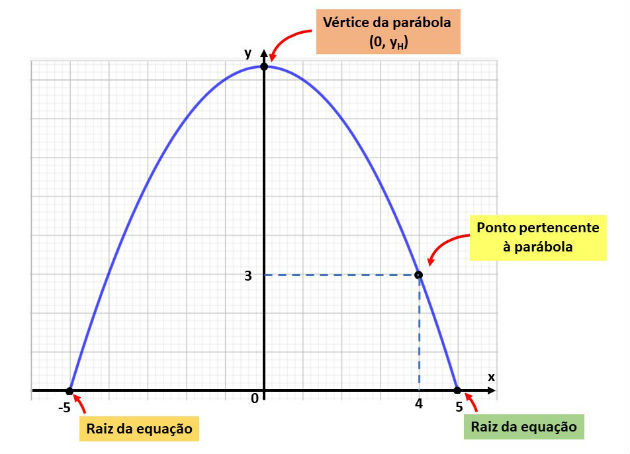
Escolhemos o eixo de simetria da parábola coincidindo com o eixo y do plano cartesiano. Assim, notamos que a altura representa o ponto (0, y_H).

Observando o gráfico da parábola, percebemos ainda, que o 5 e o -5 são as duas raízes da função e que o ponto (4,3) pertence a parábola.

Com base em todas essas informações, vamos utilizar a forma fatorada da equação do 2º grau, ou seja:

y = a . (x – x₁) . (x – x₂)

Onde:

a: coeficiente
x₁ e x₂: raízes da equação

Para o ponto x = 4 e y = 3, temos:

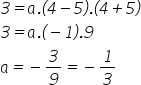
Conhecendo o valor de a, podemos calcular o valor da altura (y_H) usando novamente a forma fatorada da equação do 2º grau. Para isso, consideramos x = 0, conforme indicado no gráfico acima:

Alternativa: d) 25/3