
Um conjunto numérico é um composto, um resumo de elementos individuais. O conjunto é um dos conceitos mais importantes e fundamentais da matemática, a teoria dos conjuntos lida com a sua consideração.

A descrição de um conjunto é toda sobre a questão de quais elementos estão contidos nele. Não pergunta se um elemento está incluído mais de uma vez ou se há uma ordem entre os elementos. Um conjunto não precisa conter um elemento – existe exatamente um conjunto sem elementos, o “conjunto vazio”. Na matemática, os elementos de um conjunto são muitas vezes números, pontos de espaço ou conjuntos de quantidades. No entanto, o conceito é aplicável a qualquer objeto: Por exemplo, em estatísticas sobre amostras aleatórias, em medicina em registros médicos, na banca de mercado em um saco de frutas.
É a ordem dos elementos de importância, então é chamado um finito ou sequência infinita quando os componentes seguidores pode ser mencionado com os números naturais (o primeiro, o segundo, etc.). Consequências finais também são chamadas de tuplas. Em uma tupla ou sequência, os elementos também podem ocorrer várias vezes. Uma entidade que contém muitos elementos e, além do número de cópias de cada elemento, mas não a ordem, é chamada de conjunto múltiplo.

Quantidades numéricas foram calculadas com a ideia criada para resumir os números e suas propriedades em conjuntos. Nas primeiras organizações sociais, as pessoas já estavam confrontadas com a necessidade de compreender eventos, fatos e quantidades. Assim, cada civilização criou símbolos que representavam palavras, situações e números. A representação de conjuntos tornou-se mais complexa à medida que ocorriam menos necessidades elementares. Por exemplo, para saber a relação entre o comprimento e o diâmetro de uma circunferência.
Com os avanços no estudo da álgebra e a resolução de equações, também foi necessária uma sistematização e organização dos números em grupos (ou conjuntos). Desta forma, conjuntos numéricos foram criados. O que são números? Conjuntos numéricos são a união de elementos com atributos semelhantes. Os conjuntos de números são a união de números que possuem as mesmas características.
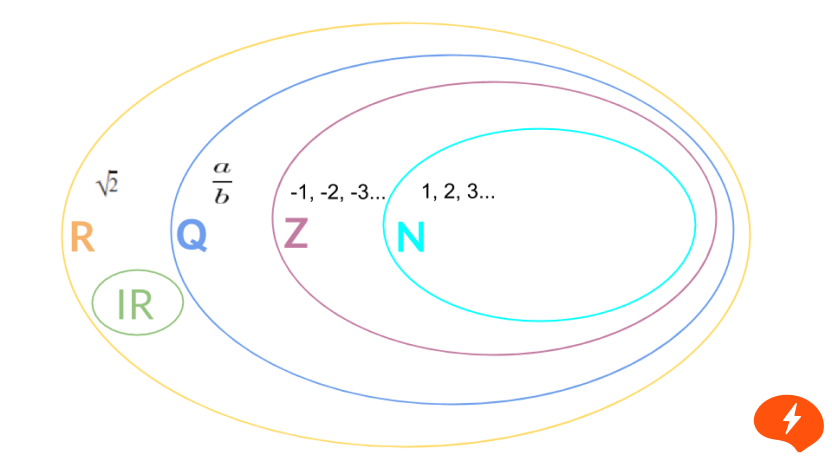
Conjunto de números naturais
Números naturais são números inteiros e positivos, incluindo zero. O conjunto de números naturais é representado por N.
N = {0, 1, 2, 3, 4 …}
Subconjunto de números naturais
Representado por N *, este conjunto representa os números naturais não nulos, isto é, sem a presença de zero.
N * = {1, 2, 3, 4 …}
Sempre que * existe em um conjunto numérico, o elemento zero não faz parte do conjunto.
Conjunto de números inteiros
Os inteiros são representados pela letra Z. Este conjunto leva em consideração todos os números naturais e negativos.
Z = {… -4, -3, -2, -1, 0, 1, 2, 3, 4 …}
Subconjuntos dos números inteiros
Inteiros não negativos
Números negativos não fazem parte desse conjunto. No entanto, este conjunto exibe zero porque é um número neutro.
Z + = {0, 1, 2, 3, 4 …}
Inteiros positivos
Este conjunto considera apenas números positivos e, portanto, zero não aparece.
Z* + = {1, 2, 3, 4 …}
Inteiros não positivos
Todos os números positivos não fazem parte do conjunto. Note que o * não existe. Portanto, zero faz parte da sentença.
Z*_ = {… -4, -3, -2, -1, 0}
Inteiros negativos
Nesta sentença, todos os números positivos e zero não fazem parte da sentença.
ℤ*_ = {… -4, -3, -2, -1}
Inteiros não nulos
O zero não está presente nesse conjunto, porém os demais números fazem parte do conjunto.
Z* = {… -4,-3, -2, -1, 1, 2, 3, 4…}
Conjunto de números racionais
Os números racionais ou o conjunto de quocientes entre dois inteiros podem todos ser representados em uma proporção.
O numerador e o denominador devem ser números inteiros e diferentes de zero. Esta frase é representada pela letra Q.

Além das frações, os números racionais podem ser decimais (0.3, 1.25) ou infinitamente periódicos (.333 ..). Natural e inteiros são subconjuntos de números racionais.
Conjunto de números irracionais
Os números irracionais representados pela letra I são aqueles que não podem ser obtidos dividindo-se dois inteiros por decimais infinitos e não-periódicos. Ou seja, não há repetições nas casas decimais. Estas são as chamadas decimais não exatas, como:
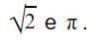
Conjunto dos Números reais
Este conjunto é representado pela letra R e inclui todos os números racionais e irracionais. Números racionais e irracionais não têm elementos comuns. Cada um pertence a uma sentença específica. Por essa razão, um conjunto tinha que ser criado para unir os dois.
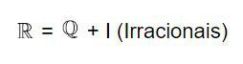
Intervalos reais
Os intervalos numéricos são subconjuntos dos números reais R.
Exemplos de áreas de números reais:
Intervalo aberto
]2, 7[ = {x ∈ R | 2< x <7}
Este intervalo é de 2 a 7, mas os números 2 e 7 não fazem parte do intervalo.
Intervalo fechado
[2, 7] = {x ∈ R | 2 ≤ x ≤7}
O intervalo varia de 2 a 7, ou seja, o intervalo é maior ou igual a 2 e menor ou igual a 7.
Intervalo determinado pela desigualdade
[2, 7 [= {x ∈ R | 2 ≤ x <7}
O intervalo é de 2 a 7, mas o 7 não pertence ao intervalo.
Intervalo aberto infinito
] 2, + ∞ [= {x ∈ R | 2> ∞}
Este intervalo contém todos os números que são maiores que 2.
Exercícios Sobre Conjuntos Numéricos
Exercício 1- Em um colégio de 100 alunos, 80 gostam de sorvete de baunilha, 70 gostam de sorvete de morango e 60 gostam dos dois sabores. Quantos não gostam de nenhum dos dois sabores?
a) 0
b) 10
c) 20
d) 30
e) 40
Resposta: 10
Exercício 2- Sejam x e y números tais que os conjuntos {0, 7, 1} e {x, y, 1} são iguais. Então, é correto afirmar que:
a) x = 0 e y = 5
b) x + y = 7
c) x = 0 e y = 1
d) x + 2 y = 7
e) x = y
Resposta: x + y = 7
Exercício 3- Uma prova com duas questões foi dada a uma classe de 40 alunos. Dez alunos acertaram as duas questões, 25 acertaram a primeira e 20 acertaram a segunda questão. Quantos alunos erraram as duas questões?
a) 40
b) 10
c) nenhum
d) 8
e) 5
Resposta: 5
Exercício 4- Supõe-se que em uma pesquisa envolvendo 660 pessoas, cujo objetivo era verificar o que elas estão lendo, obtiveram-se os seguintes resultados: 100 pessoas leem somente revistas, 300 pessoas leem somente livros e 150 pessoas leem somente jornais.
Supõe-se ainda que, dessas 660 pessoas, 80 leem livros e revistas, 50 leem jornais e revistas, 60 leem livros e jornais e 40 leem revistas, jornais e livros.
Em relação ao resultado dessa pesquisa, são feitas as seguintes afirmações:
I – Apenas 40 pessoas leem pelo menos um dos três meios de comunicação citados.
II – Quarenta pessoas leem somente revistas e livros, e não leem jornais.
III – Apenas 440 pessoas leem revistas ou livros.
Assinale a alternativa correta.
a) Somente as afirmativas I e III são verdadeiras.
b) Somente as afirmativas I e II são verdadeiras.
c) Somente as afirmativas I, II e III são verdadeiras.
d) Somente a afirmativa II é verdadeira.
e) Somente a afirmativa I é verdadeira.
Exercício 5- De acordo com o matemático Leopold Kronecker (1823-1891), “Deus fez os números inteiros, o resto é trabalho do Homem.” Os conjuntos numéricos são, como afirma o matemático, uma das grandes invenções humanas. Assim, em relação aos elementos desses conjuntos, é correto afirmar que:
a) O produto de dois números irracionais é sempre um número irracional.
b) A soma de dois números irracionais é sempre um número irracional.
c) Entre os números reais 3 e 4 existe apenas um número irracional.
d) Entre dois números racionais distintos existe pelo menos um número racional.
e) A diferença entre dois números inteiros negativos é sempre um número inteiro negativo.
Resposta: d) Entre dois números racionais distintos existe pelo menos um número racional.
Exercício 6- Um professor de Matemática, ao lecionar Teoria dos Conjuntos em uma certa turma, realizou uma pesquisa sobre as preferências clubísticas de seus n alunos, tendo chegado ao seguinte resultado:
• 23 alunos torcem pelo Paysandu Sport Club;
• 23 alunos torcem pelo Clube do Remo;
• 15 alunos torcem pelo Clube de Regatas Vasco da Gama;
• 6 alunos torcem pelo Paysandu e pelo Vasco;
• 5 alunos torcem pelo Vasco e pelo Remo.
Se designarmos por A o conjunto dos torcedores do Paysandu, por B o conjunto dos torcedores do Remo e por C o conjunto dos torcedores do Vasco, todos da referida turma, teremos, evidentemente, A ∩ B = Ø. Concluímos que o número n de alunos dessa turma é:
a) 49.
b) 50.
c) 47.
d) 45.
d) 46.
Resposta: b) 50. Para resolver essa questão, devemos desenhar os diagramas de todos os conjuntos descritos no enunciado, destacando a sua intersecção.
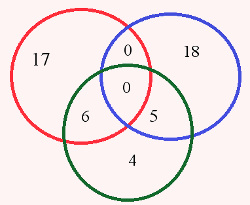
Efetuando a adição, temos que: 17 + 18 + 5 + 6 + 4 = 50
O número n de alunos dessa turma é 50. A resposta dessa questão é a alternativa “b”.
Exercício 7- Uma escola realizou uma pesquisa sobre os hábitos alimentares de seus alunos. Alguns resultados dessa pesquisa foram:
• 82% do total de entrevistados gostam de chocolate;
• 78% do total de entrevistados gostam de pizza; e
• 75% do total de entrevistados gostam de batata frita.
Então, é CORRETO afirmar que, no total de alunos entrevistados, a porcentagem dos que gostam, ao mesmo tempo, de chocolate, de pizza e de batata frita é, pelo menos, de:
a) 25%.
b) 30%.
c) 35%.
d) 40%.
Resposta:
Inicialmente devemos nomear as incógnitas da equação da questão:
x = pessoas que gostam de pizza.
y = pessoas que gostam de chocolate.
z = pessoas que gostam de batata frita.
w = pessoas que gostam de chocolate e batata frita.
s = pessoas que gostam de batata frita e pizza.
v = pessoas que gostam de chocolate e pizza.
d = pessoas que gostam ao mesmo tempo de chocolate, pizza e batata frita.
Agora que já sabemos quais são as incógnitas, vamos escrever as equações:
Gostam de chocolate: Selecionaremos todas as variáveis que possuem chocolate:
y + w + v + d = 82%
Gostam de pizza: Selecionaremos todas as variáveis que possuem pizza:
x + s + v + d = 78%
Gostam de batata frita: Selecionaremos todas as variáveis que possuem batata frita:
z + d + s + w = 75%
Agora vamos realizar a soma das equações das pessoas que gostam de chocolate com as pessoas que gostam de pizza:
y + w + v + d + x + s + v + d = 82% + 78%
y + w + v + d + x + s + ( v + d ) = 160% → Veja que y + w + v + d + x + s = 100% de pessoas.
100% + v + d = 160%
v + d = 160% – 100%
v + d = 60%
Some as equações gerais com a equação referente às pessoas que gostam de batata frita (v + d = 60%):
z + d + s + w + v + d = 75% + 60%
z + d + s + w + v + (d) = 135% → Observe que z + d + s + w + v = 100%.
100% + d = 135.
Obtemos, então, o sistema:
v + d = 60% → Primeira equação
100% + d = 135% → Segunda equação
Resolvendo a segunda equação, obtemos:
100% + d = 135%
d = 35% → Pessoas que gostam ao mesmo tempo de chocolate, batata frita e pizza.
Substituindo o valor de d na primeira equação, temos:
v + d = 60%
v + 35% = 60%
v = 25% → Pessoas que gostam de chocolate e pizza.
A resposta correta para essa questão é a alternativa “c”.
Exercício 8- Dados os conjuntos A = { 0, 1, 2, 3, 4, 5}, B = { 4, 5, 6, 7 } e C = { 4, 5, 6, 8}, descubra o resultado de: (A – C) ∩ (B – C)
A – C = {0, 1, 2, 3} → Esse é o conjunto de todos os elementos de A que não pertencem a B;
B – C = {7} → Esse é o conjunto de todos os elementos que pertencem a B e não pertencem a C;
Logo, a intersecção entre (A – C) ∩ (B – C) é vazia, visto que nenhum número se repete nesses dois conjuntos.


