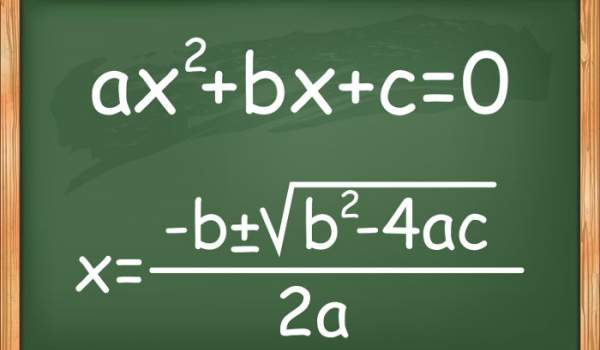
A equação de segundo grau, ou equação do 2º grau, tem este nome porque é uma equação polinomial cujo termo é elevado a um maior grau ao quadrado. Esta equação quadrática também é representada por:
ax2 + bx + c = 0
Em uma equação de segundo grau, x é o desconhecido e representa um valor desconhecido.
As letras a, b e c são chamadas coeficientes da equação.
Os coeficientes são números reais e o coeficiente a deve ser diferente de zero, caso contrário, torna-se uma equação de primeiro grau.
Resolver uma segunda equação de graus significa que você encontra valores reais de x que fazem a equação verdadeira. Esses valores são chamados de raízes da equação. Uma equação quadrática tem no máximo duas raízes reais.

Equações Completas e Incompletas de 2º grau
As equações completas de segunda ordem são aquelas com todos os coeficientes, isto é, a, b e c são diferentes de zero (a, b, c ≠ 0).
Por exemplo, a equação 5×2 + 2x + 2 = 0 está completa porque todos os coeficientes são diferentes de zero (a = 5, b = 2 ec = 2).
Uma equação quadrática é incompleta se b = 0 ou C = 0 ou b = c = 0. Por exemplo, a equação 2×2 = 0 é incompleta porque a = 2, b = 0 e c = 0

Exercícios de Equações do 2º Grau
1) Encontre os valores de x pelos quais a equação 4×2 – 16 = 0.
Solução: A equação dada é uma equação incompleta do segundo grau com b = 0. Para equações desse tipo, podemos resolver isolando x. Assim:
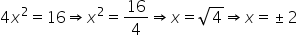
Observe que a raiz quadrada de 4 pode ser 2 e -2, pois esses dois quadrados são 4. Assim, as raízes da equação são 4×2-16 = 0x = -2 e x = 2
2) Encontre o valor de x de forma que a área do retângulo abaixo dele seja igual a 2.
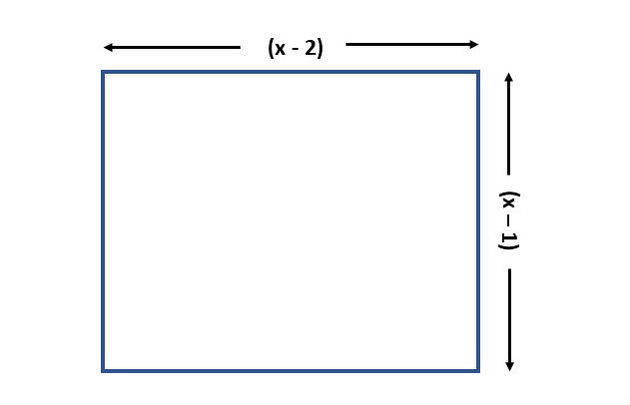
Solução:
A área do retângulo é determinada multiplicando a base pela altura. Portanto, precisamos multiplicar os valores fornecidos e corresponder a 2. (X-2). (x = 1) = 2
Agora vamos multiplicar todos os termos: x. x -1. x – 2. x – 2. (- 1) = 2 x2 – 1x – 2x + 2 = 2 x2-3x + 2-2 = 0 x2 – 3x = 0 .Tendo resolvido as multiplicações e simplificações, encontramos uma equação incompleta do segundo grau com c = 0.
Este tipo de equação pode ser resolvido por fatoração, uma vez que x é repetido em ambos os termos. Então, vamos provar isso. x. (x – 3) = 0 Se o produto for zero ou x = 0 ou (x – 3) = 0. No entanto, se você substituir x por zero, as medidas nas laterais serão negativas, portanto esse valor não é a resposta para a pergunta.
Então temos o único resultado possível (x – 3) = 0. Solução dessa equação: x = 3 = 0 x = 3 . Assim, o valor do x para que a área do retângulo seja igual a 2 é x = 3.

Fórmula de Bhaskara
Quando uma equação de segundo grau é concluída, usamos a fórmula de Bhaskara para encontrar as raízes da equação.
A fórmula é mostrada abaixo:
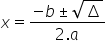
Fórmula do Delta
Na fórmula de Bhaskara, a letra grega Δ (delta), que é chamada de discriminante da equação, aparece porque, de acordo com seu valor, é possível saber o número de raízes da equação.
Para calcular o delta, usamos a seguinte fórmula:
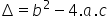
Passo a passo
Para resolver uma equação de segundo grau usando a fórmula de Bhaskara, precisamos fazer o seguinte:
Etapa 1: Identifique os coeficientes a,b e c.
Os termos da equação nem sempre aparecem na mesma ordem. Portanto, é importante identificar os coeficientes, independentemente da ordem em que eles estão localizados.
O coeficiente a é o número que está junto com x2, b é o número que acompanha x e c é o termo independente, ou seja, o número que aparece sem x.
Etapa 2: calcule o delta.
Para calcular as raízes, o valor do delta deve ser conhecido. Para fazer isso, substituímos as letras na fórmula pelos valores dos coeficientes.
A partir do valor delta podemos conhecer antecipadamente o número de raízes que terão a equação do segundo grau. Ou seja, se o valor de Δ for maior que zero (Δ> 0), a equação terá duas raízes reais e diferentes.
Se, por outro lado, Delta for menor que zero (Δ), então a equação não tem raízes reais e se for igual a zero (Δ = 0), então a equação representa apenas uma raiz.
Etapa 3: calcule as raízes.
Se o valor encontrado para Delta for negativo, você não precisa fazer mais nenhum cálculo, e a resposta é que a equação não tem raízes verdadeiras.
Se o valor delta for igual ou maior que zero, devemos substituir todas as letras por seus valores na fórmula de Bhaskara e calcular as raízes.