
Equação de segundo grau são as equações na forma ax2 + bx + c = 0, com a, b e c números reais e a ≠ 0. Existem diversos métodos para resolver esse tipo de equação.
Através da fórmula de Bhaskara, conseguimos resolver exercícios sobre equação do 2º grau.
Exercício 1
Identifique os coeficientes de cada equação e diga se ela é completa ou não:
a) 5x² – 3x – 2 = 0
b) 3x² + 55 = 0
c) x² – 6x = 0
d) x² – 10x + 25 = 0
Resposta
Resposta a:
a = 5 ; b = -3 ; c = -2
Equação completa
Resposta b:
a = 3 ; b = 0 ; c = 55
Equação incompleta
Resposta c:
a = 1 ; b = -6 ; c = 0
Equação incompleta
Resposta d:
a = 1 ; b = -10 ; c = 25
Equação completa
Exercício 2
Aplicando a fórmula de Bhaskara, resolva as seguintes equações do 2º grau.
a) 3x² – 7x + 4 = 0
b) 9y² – 12y + 4 = 0
c) 5x² + 3x + 5 = 0
Resposta
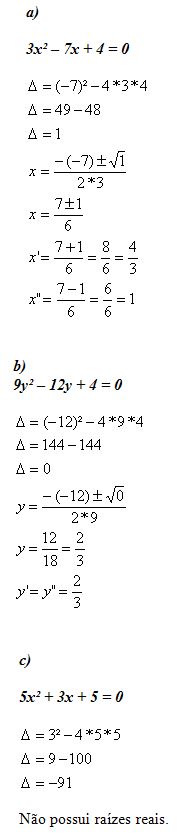
Exercício 3
Resolva a equação: 4x2 + 8x + 6 = 0
Resposta
Os coeficientes da equação são: a = 4, b = 8, c = 6. Substituindo esses valores na fórmula de Bhaskara, temos:
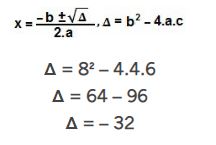
Como Δ < 0, a equação não possui raiz real.
Exercício 4
Ache as raízes das equações:
a) x2 – x – 20 = 0
b) x2 – 3x -4 = 0
c) x2 – 8x + 7 = 0
Resposta

Exercício 5
Determine quais os valores de k para que a equação 2x² + 4x + 5k = 0 tenha raízes reais e distintas.
Resposta
Uma equação do 2º grau possui duas raízes reais e distintas quando ∆ > 0, então:
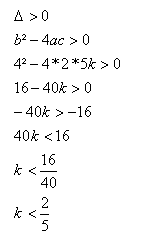
Exercício 6
Encontre as raízes da equação: x2 – 4x – 5 = 0
Resposta
Os coeficientes dessa equação são: a = 1, b = – 4, c = – 5. Agora basta aplicar esses valores na fórmula de Bhaskara:
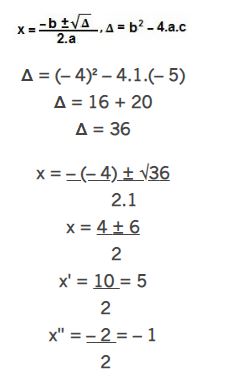
Nesse caso, a equação tem duas raízes reais: – 1 e 5.
Exercício 7
Dentre os números -2, 0, 1, 4, quais deles são raízes da equação x²-2x-8= 0?
Resposta

Exercício 8
Se v e w são as raízes da equação x2 + ax + b = 0, em que a e b são coeficientes reais, então v2 + w2é igual a:
a) a2 – 2b
b) a2 + 2b
c) a2 – 2b2
d) a2 + 2b2
e) a2 – b2
Resposta
Ao identificar os coeficientes da equação, encontramos: A = 1, B = ae C = b. Agora basta aplicar esses valores na fórmula de Bhaskara. Para não nos confundirmos, neste exercício utilizaremos letras maiúsculas na fórmula de Bhaskara. Ao substituir os coeficientes, utilizaremos letras minúsculas como de costume:
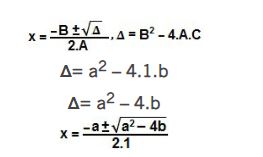
Essa equação terá duas raízes, o que as diferenciará será o sinal ± que antecede a raiz quadrada. Então, iremos considerar como v o resultado com a raiz quadrada positiva e como w o resultado com a raiz quadrada negativa. A soma dos quadrados de v e w é dada por:
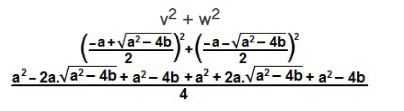
Como possuem sinais opostos, os dois termos com raiz serão cancelados, restando apenas:
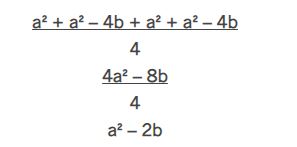
Portanto, a alternativa correta é a letra a.
Exercício 9
Calcule o valor de p na equação x² – (p + 5)x + 36 = 0, de modo que as raízes reais sejam iguais.
Para essa condição, o valor de ∆ precisa ser igual a 0.
Resposta
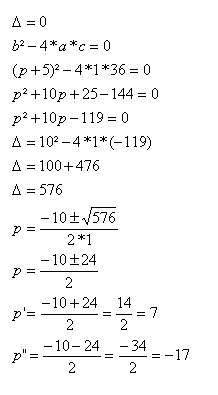
Exercício 10
Resolva a seguinte equação do 2º grau.
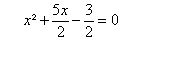
Resposta
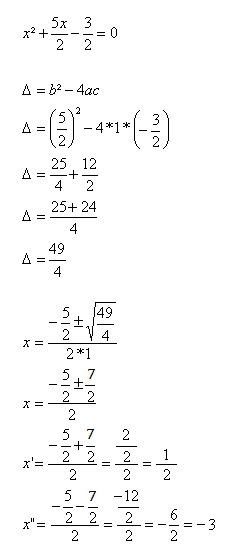
Exercício 11
A soma de um número racional não inteiro com o dobro do seu inverso multiplicativo é 33/4. Esse número está compreendido entre:
a) 5 e 6
b) 1 e 5
c) 1/2 e 1
d) 3/10 e 1/2
e) 0 e 3/10
Resposta
Chamaremos por x o número que estamos procurando, seu inverso multiplicativo é 1/x. Se a soma de x com o dobro de seu inverso multiplicativo é 33/4, teremos:

Para resolver essa equação do 2° grau, utilizaremos a fórmula de Bhaskara:
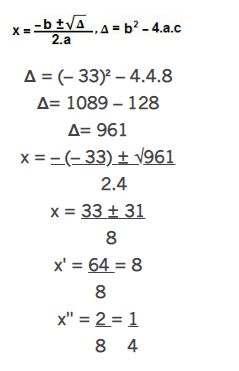
Encontramos duas raízes para a equação, mas observe que o exercício refere-se apenas à raiz que é um número racional não inteiro, portanto, o primeiro resultado não é interessante, pois 8 é um número inteiro. Sendo assim, utilizaremos o valor de x”, uma vez que ¼ = 0,25.
A alternativa correta é a letra e, pois ¼ é maior que zero e é menor que 3/10, que equivale a 0,3.
O que você achou dos exercícios? Deixe nos comentários a sua opinião e vote nas estrelinhas!


muito bom os exercicios