Uma função para ser do 2º grau precisa assumir algumas características, pois ela deve ser dos reais para os reais, definida pela fórmula f(x) = ax2 + bx + c, sendo que a, b e c são números reais com a diferente de zero. Concluímos então, que a condição para que uma função seja do 2º grau é que o valor de a, da forma geral, não pode ser igual a zero.
A definição de função do 2º grau é:
f: R→ R definida por f(x) = ax2 + bx + c, com a ? R* e b e c ? R.
Em uma função do segundo grau, os valores de b e c podem ser iguais a zero, quando isso ocorrer, a equação do segundo grau será considerada incompleta.
Exemplos
- f(x) = 3x2 – 4x + 1, onde a = 3, b = – 4 e c = 1
- f(x) = x2 -1, onde a = 1, b = 0 e c = -1
- f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
- f(x) = – x2 + 8x, onde a = -1, b = 8 e c = 0
- f(x) = -4x2, onde a = – 4, b = 0 e c = 0
Resolvendo uma Função
Confira o passo-a-passo por meio um exemplo de resolução de função quadrática:
Exemplo:
Determine a, b e c na função quadrática dada por: f(x) = ax2 + bx + c, sendo:
f (–1) = 8
f (0) = 4
f (2) = 2
Primeiramente, vamos substituir o x pelos valores de cada função e assim teremos:
f (–1) = 8
a (–1)2 + b (–1) + c = 8
a – b + c = 8 (equação I)
f (0) = 4
a . 02 + b . 0 + c = 4
c = 4 (equação II)
f (2) = 2
a . 22 + b . 2 + c = 2
4a + 2b + c = 2 (equação III)
Pela segunda função f (0) = 4, já temos o valor de c = 4. Assim, vamos substituir o valor obtido para c nas equações I e III para determinar as outras incógnitas (a e b):
(Equação I)
a – b + 4 = 8
a – b = 4
a = b + 4
Já que temos a equação de a pela Equação I, vamos substituir na III para determinar o valor de b:
(Equação III)
4a + 2b + 4 = 2
4a + 2b = – 2
4 (b + a) + 2b = – 2
4b + 16 + 2b = – 2
6b = – 18
b = – 3
Por fim, para encontrar o valor de a substituímos os valores de b e c que já foram encontrados. Logo:
(Equação I)
a – b + c = 8
a – (– 3) + 4 = 8
a = – 3 + 4
a = 1
Sendo assim, os valores das incógnitas da função quadrática dada são:
a = 1
b = – 3
c = 4
Gráfico
Os gráficos das funções polinomiais são representados por curvas, chamadas de parábolas.
Dependendo do valor de a na expressão y = ax2 + bx + c, a parábola pode ser:
- a > 0: a parábola apresenta uma concavidade voltada para cima.
- a : a parábola apresenta uma concavidade voltada para baixo.
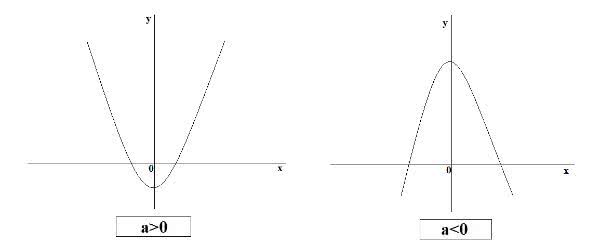
Sendo assim, o valor de a vai definir a concavidade da parábola.
A partir dos pares ordenados dados (x; y), podemos construir a parábola num plano cartesiano, por meio da ligação entre os pontos encontrados.
Obs: o gráfico da função do 1º grau é representado por uma reta e não parábola.
Exercícios
Exercício 1
Calcule o valor de k de modo que a função f(x) = 4x² – 4x – k não tenha raízes, isto é, o gráfico da parábola não possui ponto em comum com o eixo x.
Resposta

Exercício 2
Determine os valores de m, para que a função f(x) = (m – 2)x² – 2x + 6 admita raízes reais.
Resposta

Exercício 3
O gráfico da função quadrática definida por y = x² – mx + (m – 1), em que m Є R, tem um único ponto em comum com o eixo das abscissas. Determine y associado ao valor de x = 2.
Resposta

Exercício 4
Determine os pontos de intersecção da parábola da função f(x) = 2x² – 3x + 1, com o eixo das abscissas.
Resposta

O que você achou dos exercícios? Deixe o seu comentário e vote nesse artigo clicando nas estrelinhas!